Seite zuletzt aktualisiert: 23.06.2023
Aufgabenstellung
Gegeben sind zwei Geraden g und h im \(\, \mathbb{R}^3 \).
Die Gerade g ist durch den Stützpunkt \(\, P \,\) und den Richtungsvektor \(\, \vec u \,\) festgelegt,
die Gerade h durch den Stützpunkt \(\, Q \,\) und den Richtungsvektor \(\, \vec v \,\).
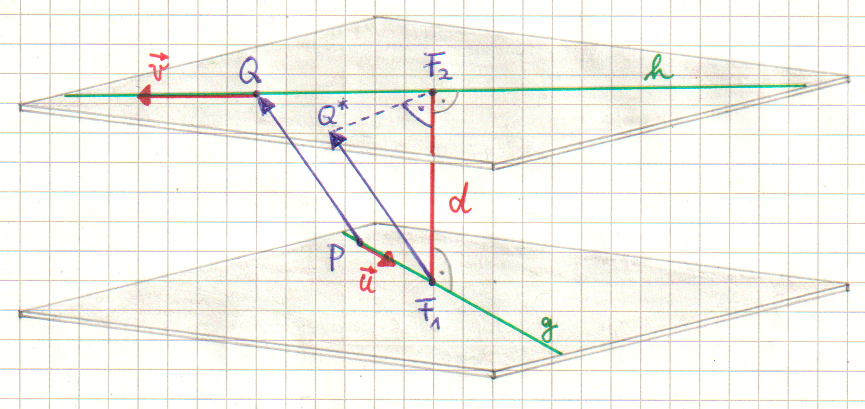
Es soll der (minimale) Abstand d dieser beiden Geraden berechnet werden.
* * *
Lösungsidee
Es wird zunächst ein Vektor \(\, \vec n \,\) ermittelt, der orthogonal zu beiden Richtungsvektoren \(\, \vec u \,\) und \(\, \vec v \,\) ist. Dieser kann z. B. mit Hilfe des Kreuzproduktes von \(\, \vec u \,\) und \(\, \vec v \,\) berechnet werden.
Die Richtung des Vektors \(\, \vec n \,\) ist identisch mit der Richtung von \(\, \overrightarrow{F_1 F_2} \,\). Mit dem Vektor \(\, \vec n \,\) hat man sozusagen die Richtung der kürzesten Abstandslinie d bestimmt.
Im zweiten Schritt wird der Vektor \(\, \overrightarrow{PQ} \,\) auf \(\, \vec n \,\) projiziert. Man erhält einen Vektor \(\, \vec d \,\), dessen Länge der gesuchte Abstand d ist.
Dass die Projektion von \(\, \overrightarrow{PQ} \,\) auf \(\, \vec n \,\) zum Vektor \(\, \vec d \,\) führt, sieht man besser, wenn man den Ansatzpunkt des Vektors \(\, \overrightarrow{PQ} \,\) vom Punkt \(\, P \,\) zum Punkt \(\, F_1 \,\) verschiebt. Es ist \(\, \overrightarrow{PQ} = \overrightarrow{F_1 Q^*} \,\).
* * *
Berechnung
Um die Länge d des projizierten Vektors \(\, \vec d \,\) zu berechnen, verwenden wir die Formel (5) aus ▸HNF - Teil 3.
\( \vert \vec d \vert = \frac{\vert \overrightarrow{PQ} \,\cdot\, \vec n\vert}{|\vec n| } \,\) mit \(\, \vec n = \vec u \times \vec v \,\),
wobei \(\, \vec p \,\) und \(\, \vec q \,\) die Ortsvektoren der Stützpunkte \(\, P \,\) und \(\, Q \,\) sind.
In diese Formel setzen wir \(\, \overrightarrow{PQ} = \vec q - \vec p \,\) sowie \(\, \vec n = \vec u \times \vec v \,\) ein und erhalten:
\( d = \frac{|\, (\vec q - \vec p) \,\cdot\, (\vec u \times \vec v) \,|}{\left| \vec u \times \vec v \right| } \,\)
* * *
Sonderfall: Parallele Geraden
Sollte das Vektorprodukt \(\, \vec u \times \vec v \,\) null ergeben, heißt dies, dass die Geraden nicht windschief, sondern parallel bzw. identisch sind.
In diesem Fall ist die Formel für den Abstand paralleler Geraden anzuwenden, siehe ▸Abstand paralleler Geraden.