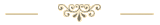Seite zuletzt aktualisiert: 22.06.2023
Die Hessesche Normalform lautet:
\( (\vec x - \vec q) \cdot \vec n_0 = 0 \,\).
Der Term auf der linken Seite der Hesseschen Normalform ist der Term für den Abstand \( a \) eines Punktes X (mit Ortsvektor \( \vec x \,\)) von der Ebene E (ohne die Betragsstriche).
Der Vektor \( \vec q \,\) ist ein Stützvektor der Ebene E.
Die Hessesche Normalform besagt nichts anderes als \(\, a = 0 \,\).
* * *
Vorgehensweise
Es wird der Abstand \(a\) des Punktes X von der Ebene E berechnet.
Der Punkt X liegt genau dann in der Ebene E, wenn \(\,a = 0\,\) ist.
* * *
Überlegung
Der Differenzvektor \(\, \vec x - \vec q \,\) wird auf die Normalenrichtung (rote Linie) projiziert. Als Ergebnis der Projektion erhält man den Vektor \(\, \vec p \). Die Länge des Vektors \(\, \vec p \,\) ist der Abstand des Punktes X von der Ebene E (siehe Zeichnung oben):
\( a = |\vec p| \)
Es muss also \(\, |\vec p| \,\) berechnet werden.
* * *
Berechnung von \( a \,\) bzw. \( |\vec p| \,\)
Setzt man in Formel (2) aus ▸TEIL 3 für \( \vec x \) den Differenzvektor \( \vec x - \vec q \) ein, so erhält man:
\( \lambda = (\vec x - \vec q) \cdot \vec n_0 \)
Setzt man Betragsstriche und beachtet, dass \(\, |\lambda| = |\vec p| \,\) ist, erhält man daraus:
\( |\vec p| = |(\vec x - \vec q) \cdot \vec n_0| \)
Diese Formel berechnet also den Abstand des Punktes X von der Ebene E:
\( a = |(\vec x - \vec q) \cdot \vec n_0| \) (1) (Abstandsformel)
* * *
Hessesche Normalform
Wie oben bereits dargelegt, liegt der Punkt X genau dann in der Ebene E, wenn der Abstand \(\,a = 0\,\) ist. Das heißt, der Ausdruck innerhalb der Betragsstriche muss null sein:
\( (\vec x - \vec q) \cdot \vec n_0 = 0 \) (2)
Diese Gleichung heißt Hessesche Normalform der Ebenengleichung.
Alle Punkte X, die diese Gleichung erfüllen, liegen in der Ebene E.
Wenn man die Klammer ausmultipliziert, erhält man weitere Darstellungsformen der Hesseschen Normalform:
\( \vec x \cdot \vec n_0 - \vec q \cdot \vec n_0 = 0 \) (3)
\( \vec x \cdot \vec n_0 - d = 0 \) (4)
\( \vec x \cdot \vec n_0 = d \) (5)
* * *
Zusatzbemerkung
\( |d| \) ist der Abstand des Ursprungs von der Ebene.
Warum?
Wenn man in der Abstandsformel (1) für \(\, \vec x \,\) den Nullvektor einsetzt, erhält man
\( a = |\vec q \cdot \vec n_0| = |d| \)
* * *
Hessesche Normalform im \( \mathbb{R}^2 \)
Im Zweidimensionalen sieht die Zeichnung so aus:
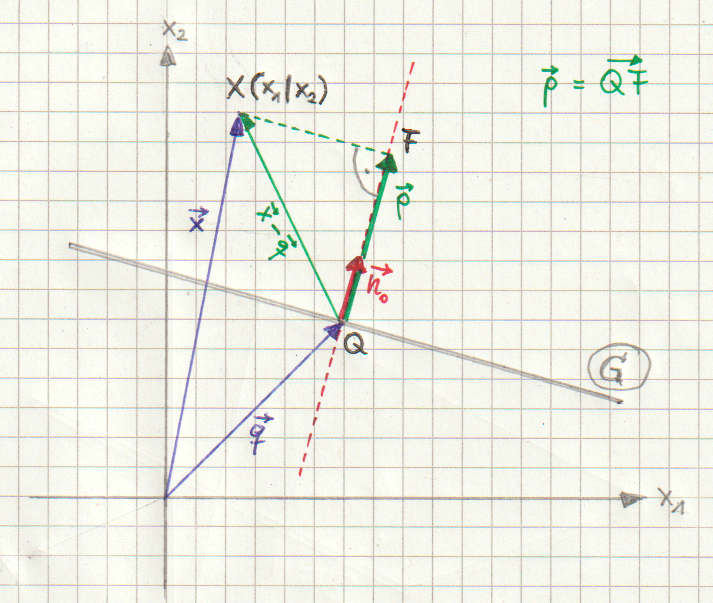
An die Stelle der Ebene E tritt eine Gerade G.
Die Rechnung ist dieselbe.