Seite zuletzt aktualisiert: 14.01.2025
Diese etwas umfangreichere Herleitung der Cardanischen Formeln kann auch als ▸PDF heruntergeladen werden.
(Letzte Änderung: 14.01.2025)
Problemstellung
Es sollen die Nullstellen eines Polynoms dritten Grades bestimmt werden:
\( x^3+a\,x^2+b\,x+c=0 \)
(Der Koeffizient von \( x^3 \) kann immer auf \( 1 \) gebracht werden.)
Die Mathematiker Paolo Ruffini (unvollständiger Beweis 1799) und Niels Henrik Abel (vollständiger Beweis 1824) konnten beweisen, dass für Polynome fünften und höheren Grades keine "elementare" Lösung mit Hilfe von Wurzeltermen existiert (Satz von Abel-Ruffini 1824).
Für Polynome dritten und vierten Grades gibt es also Lösungsformeln so wie die pq-Formel im Falle von Polynomen zweiten Grades. Die Lösungsformeln für Polynome dritten Grades sollen im Folgenden hergeleitet werden. Sie wurden zu Ehren des Mathematikers Gerolamo Cardano (1501 - 1576) "Cardanische Formeln" oder auch "Cardanosche Formeln" genannt.
Die Herleitung ist sehr ausführlich gehalten mit möglichst verständlicher Erklärung aller Schritte. Für das Verständnis reichen mathematische Grundkenntnisse aus der Schule (Terme mit reellen Variablen und reellwertige Funktionen) plus Grundkenntnisse der komplexen Zahlen, zum Beispiel ▸Komplexe Zahlen, Teil 1 bis 3. Mehrere konkrete Beispiele runden das Thema ab.
* * *
Hinweise
Für Leser, die nur an den Lösungsformeln interessiert sind, gibt es am Ende dieser Seite eine ▸Zusammenfassung.
Eine Formulierung der Cardanischen Formeln findet man ▸hier.
Wer nur an den Lösungen interessiert ist, findet hier den passenden ▸Online-Rechner.
Dieser Online-Rechner berechnet nicht nur die reellen, sondern gegebenenfalls auch die komplexen Lösungen.
* * *
1. Schritt:
Quadratisches Glied eliminieren
Ein Polynom dritten Grades kann immer in eine Form ohne quadratischen Summanden gebracht werden.
Dies erreicht man mit der Substitution
\( x = z - \frac{1}{3}a \)
Daraus ergibt sich:
\( (z - \frac{1}{3}a)^3 + a\,(z - \frac{1}{3}a)^2 + b\,(z - \frac{1}{3}a) + c = 0 \)
\( z^3 - z^2a + \frac{1}{3}za^2 - \frac{1}{27}a^3 + a(z^2 - \frac{2}{3}za + \frac{1}{9}a^2) + b(z - \frac{1}{3}a) + c = 0 \)
\( z^3 \color{#c00}{- z^2a} + \frac{1}{3}za^2 - \frac{1}{27}a^3 \color{#c00}{+ z^2a} - \frac{2}{3}za^2 + \frac{1}{9}a^3 + bz - \frac{1}{3}ab + c = 0 \)
Die Summanden mit \( z^2 \) fallen weg.
Zusammenfassen:
\( z^3 - \frac{1}{3}za^2 + bz + \frac{2}{27}a^3 - \frac{1}{3}ab + c = 0 \)
\( z^3 + (\underbrace{\color{#1478c8}{b - \frac{1}{3}a^2}}_{=\,p})z + (\underbrace{\color{#14c868}{\frac{2}{27}a^3 - \frac{1}{3}ab + c}}_{=\,q}) = 0 \)
Damit haben wir die Form
\( z^3 + pz + q = 0 \)
mit \( p = \color{#1478c8}{b - \frac{1}{3}a^2} \)
und \( q = \color{#14c868}{\frac{2}{27}a^3 - \frac{1}{3}ab + c} \) .
Zwischenresümee:
Wir haben die Gleichung dritten Grades in eine Form ohne quadratisches Glied umgewandelt:
\( z^3 + pz + q = 0 \)
Man nennt dies die "reduzierte Form" der kubischen Gleichung.
Die Koeffizienten \( p \) und \( q \) sind gegeben, denn wir können sie aus den ursprünglichen Koeffizienten \( a \) , \( b \) und \( c \) berechnen:
\( p = b - \frac{1}{3}a^2 \)
\( q = \frac{2}{27}a^3 - \frac{1}{3}ab + c \)
Die Variable \( z \) ist nun die gesuchte Größe.
Hat man die Lösungen für \( z \) berechnet, erhält man die gesuchten Lösungen mit der Formel
\( x = z - \frac{1}{3}a \) .
* * *
2. Schritt:
Lösen der Gleichung \( z^3 + pz + q = 0 \)
Um an dieser Stelle weiter zu kommen, braucht es einen genialen Einfall. Und dies ist wieder einmal eine Substitution, diesmal aber eine Substitution der besonderen Art. Man sehe und staune:
\( z = u + v \)
Statt einer Unbekannten haben wir plötzlich zwei Unbekannte! Was soll das bringen? Außerdem haben wir ja nur eine Gleichung - und jetzt zwei Unbekannte??
Dieser Trick wird von den Mathematikern des öfteren verwendet. Dadurch, dass zwischen u und v noch keine Beziehung (keine Abhängigkeit, keine zweite Gleichung) festgelegt ist, haben wir alle Freiheiten, dies nach eigenem Gutdünken zu tun. Und genau diese Freiheit bringt den entscheidenden und bahnbrechenden Vorteil. Schauen wir's uns an:
Unsere Gleichung dritten Grades sieht nach der ominösen Substitution so aus:
\( (u + v)^3 + p(u + v) + q = 0 \)
\( u^3 + 3u^2v + 3uv^2 + v^3 + p(u + v) + q = 0 \)
\( u^3 + v^3 + 3uv(u + v) + p(u + v) + q = 0 \)
\( u^3 + v^3 + (3uv + p)(u + v) + q = 0 \)
Nun ist der entscheidende Moment gekommen, unsere Freiheit in der Wahl einer zweiten Gleichung auszunutzen. Wählen wir
\( 3uv + p = 0 \) ,
so fällt der komplette dritte Summand weg:
\( u^3 + v^3 + (\underbrace{\color{#1478c8}{3uv + p}}_{=\,0})(u + v) + q = 0 \)
\( u^3 + v^3 + q = 0 \)
Das Bahnbrechende:
Die Unbekannten \( u \) und \( v \) kommen nun nicht mehr in erster und dritter Potenz vor, sondern nur noch in der dritten Potenz.
Zwischenstand:
Statt eine Lösung für die Variable \( z \) in der Gleichung
\( z^3 + pz + q = 0 \)
zu suchen, suchen wir jetzt eine Lösung für die beiden Unbekannten \( u \) und \( v \) in einem Gleichungssystem bestehend aus den beiden Gleichungen
\( (1) \qquad u^3 + v^3 + q = 0 \)
\( (2) \qquad 3uv + p = 0 \)
Lösung des Gleichungssystems:
\( (2) \quad \Rightarrow \quad 3uv + p = 0 \quad \Rightarrow \quad v = - \frac{p}{3u} \quad \Rightarrow \quad v^3 = - \frac{p^3}{27u^3} \)
Einsetzen in \( (1) \) :
\( u^3 - \frac{p^3}{27u^3} + q = 0 \qquad |\,\cdot u^3 \)
\( (\color{#1478c8}{u^3})^2 + q\,\color{#1478c8}{u^3} - (\frac{p}{3})^3 = 0 \)
In dieser Gleichung ist \( u \) die einzige Unbekannte. Die Variablen \( p \) und \( q \) sind ja die vorgegebenen Koeffizienten unserer Gleichung dritten Grades.
Und wenn wir genau hinschauen, haben wir eine quadratische Gleichung für \( u^3 \), die uns zwei Lösungen für \( u^3 \) liefert.
Wem der letzte Satz nicht einleuchtend erscheint, kann die Substitution \( \color{#1478c8}{t = u^3} \) vornehmen und erhält die quadratische Gleichung
\( \color{#1478c8}{t}^2 + q\,\color{#1478c8}{t} - (\frac{p}{3})^3 = 0 \) .
(Diese Gleichung nennt man übrigens die quadratische Resolvente der ursprünglichen kubischen Gleichung.)
Ich möchte aber keine neue Variable ins Spiel bringen und schreibe im Folgenden statt \( \color{#c00}{t_{1,2}} \) lieber \( \color{#c00}{(u^3)_{1,2}} \) .
Die beiden Lösungen der quadratischen Gleichung sind:
\( (u^3)_{1,2} = -\frac{q}{2} \pm \sqrt{(\frac{q}{2})^2 + (\frac{p}{3})^3} \)
Die Lösungen für \( v^3 \) ergeben sich durch Umformen der Gleichung \( (1) \) des Gleichungssystems:
\( (1) \qquad u^3 + v^3 + q = 0 \)
\( v^3 = -u^3 - q \)
Die beiden Lösungen für \( u^3 \) werden eingesetzt:
\( (v^3)_{1,2} = -(-\frac{q}{2} \pm \sqrt{(\frac{q}{2})^2 + (\frac{p}{3})^3}) - q \)
\( (v^3)_{1,2} = -\frac{q}{2} \mp \sqrt{(\frac{q}{2})^2 + (\frac{p}{3})^3} \)
Das erste Lösungspaar ist \( (u^3)_1 \) und \( (v^3)_1 \) . Das zweite Lösungspaar ist \( (u^3)_2 \) und \( (v^3)_2 \) .
Vergleicht man beide Paare, stellt man fest, dass dieselben Zahlen herauskommen, nur die Variablen \( u \) und \( v \) tauschen die Rollen. Wir erhalten mit dem zweiten Lösungspaar also keine neue Lösung. Das heißt, wir können das Plusminus vor der Wurzel weglassen und uns dafür entscheiden, dass bei \( u^3 \) die Wurzel mit positivem Vorzeichen steht und bei \( v^3 \) die Wurzel mit negativem Vorzeichen. Umgekehrt wäre genauso gut möglich, aber nichts Neues.
Fazit:
Für \( u^3 \) und \( v^3 \) haben wir nun die Lösung
\( u^3 = -\frac{q}{2} + \sqrt{(\frac{q}{2})^2 + (\frac{p}{3})^3} \\ v^3 = -\frac{q}{2} - \sqrt{(\frac{q}{2})^2 + (\frac{p}{3})^3} \)
Dies sind die Cardanischen Formeln.
Falsche Schlussfolgerung:
Wer an dieser Stelle denkt "Super! Nur noch dritte Wurzel ziehen und mit \( z = u + v \) haben wir die Lösung!", der ist auf dem Holzweg.
Auch die mitunter publizierte Formel
\( z = u + v = \sqrt[3]{-\frac{q}{2} + \sqrt{(\frac{q}{2})^2 + (\frac{p}{3})^3}} + \sqrt[3]{-\frac{q}{2} - \sqrt{(\frac{q}{2})^2 + (\frac{p}{3})^3}} \)
ist mathematisch nicht korrekt.
Denn die erste kubische Wurzel hat im Komplexen drei Lösungen (\( u_1 \) , \( u_2 \) , \( u_3 \)), die zweite kubische Wurzel ebenfalls (\( v_1 \) , \( v_2 \) , \( v_3 \)). Welche von den Lösungen für \( u \) werden in dieser Formel mit welchen von den Lösungen für \( v \) addiert? Theoretisch gibt es hier neun Möglichkeiten, eine Summe der Form \( u + v \) zu bilden.
Dagegen könnte nun das Argument kommen: "Wir rechnen nur mit reellen Zahlen. Da hat jede Kubikwurzel maximal ein Ergebnis. Und wenn unter der inneren Quadratwurzel etwas Negatives steht, gibt es halt keine reelle Lösung."
Insbesondere der letzte Satz ist ein schwerer Irrtum. Gerade in den Fällen, wo drei reelle Lösungen herauskommen, stehen unter den Quadratwurzeln negative Radikanden. Man muss also mit komplexen Zahlen weiterrechnen, um dann das Kuriose zu erleben, dass sich am Ende trotzdem reelle Lösungen ergeben.
Wir sind hier an einem Punkt, der als die Geburtsstunde der komplexen Zahlen angesehen werden kann.
Der Mathematiker Gerolamo Cardano staunte vermutlich auch nicht schlecht, als er damals im 16. Jahrhundert einfach mal probeweise mit dem Symbol \( \sqrt{-1} \) weiter rechnete (was für die damalige Zeit eine nicht existierende, also eine nur eingebildete, imaginäre Zahl war), und dann feststellte, dass diese nicht existierende Zahl aus der Rechnung wieder herausfiel und sich drei reelle Lösungen ergaben, die sich bei der Probe sogar als richtig erwiesen!
Richtige Schlussfolgerung:
Wir müssen also zunächst in der Menge der komplexen Zahlen weiterrechnen und schauen, welche reellen und komplexen Lösungen herauskommen. In der Menge der komplexen Zahlen hat jede dritte Wurzel genau drei Lösungen (siehe ▸Komplexe_Zahlen, Teil 3).
Nun stellt sich die Frage, welche der drei Lösungen \( u_1 \) , \( u_2 \) , \( u_3 \) mit welcher der drei Lösungen \( v_1 \) , \( v_2 \) , \( v_3 \) zu einer Lösung für \( z \) addiert werden soll:
\( z_n = u_i + v_j \qquad ?? \)
Theoretisch gibt es neun Kombinationsmöglichkeiten. Wir wissen aber bereits, dass ein Polynom dritten Grades höchstens drei Nullstellen besitzt.
Bei der Herleitung der Cardanischen Formeln sind wir von den beiden Gleichungen
\( (1) \qquad u^3 + v^3 + q = 0 \)
\( (2) \qquad 3uv + p = 0 \)
ausgegangen, haben aber die Gleichung \( (2) \) nur in der Form \( v^3 = - \frac{p^3}{27u^3} \) verwendet, also die dritte Potenz der ursprünglichen Gleichung. Aus dem Reellen kennen wir den Effekt, dass eine quadrierte Gleichung mehr Lösungen hat als die ursprüngliche Gleichung. Im Komplexen hat auch die dritte Potenz einer Gleichung mehr Lösungen als die ursprüngliche Gleichung.
Wir haben deshalb zu prüfen, welche der neun Kombinationen \( u_i + v_j \) die (ursprüngliche) Gleichung \( (2) \) erfüllen. Es wird sich herausstellen, dass dies genau drei von den neun Kombinationen sind.
Weitere Vorgehensweise:
Es gibt zwei Möglichkeiten:
1. Möglichkeit:
Wir berechnen die dritten Wurzeln \( u_1 \) , \( u_2 \) , \( u_3 \) sowie \( v_1 \) , \( v_2 \) , \( v_3 \) mit der üblichen Methode (siehe ▸Komplexe_Zahlen, Teil 3) und prüfen, welche der neun Kombinationen \( u_i + v_j \) die ursprüngliche Gleichung \( (2) \) , also \( 3uv + p = 0 \) , erfüllen.
2. Möglichkeit:
Wir versuchen, mit Hilfe von Fallunterscheidungen weitere allgemeine Kenntnisse über die Lösungen zu gewinnen, um für jeden möglichen Fall eindeutige Lösungsformeln zu erhalten.
Zunächst soll die erste Möglichkeit anhand eines konkreten Beispiels illustriert werden. Danach wird die zweite Möglichkeit ausführlich behandelt, d.h. die Formeln der üblichen Fallunterscheidungen werden hergeleitet.
Beispiel zur 1. Möglichkeit: \( x^3 + 2x^2 - x - 2 = 0 \)
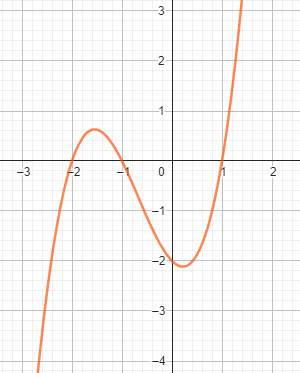
Mit \( a=2 \) , \( b=-1 \) , \( c=-2 \) folgt:
\( p = -\frac{7}{3} \)
\( q = -\frac{20}{27} \) .
Für \( u^3 \) und \( v^3 \) ergeben sich komplexe Zahlen:
\( u^3 = \frac{10}{27} + i \cdot \frac{1}{3}\sqrt{3} \)
\( v^3 = \frac{10}{27} - i \cdot \frac{1}{3}\sqrt{3} \) .
Berechnet man nun die dritten Wurzeln von \( u^3 \) und die dritten Wurzeln von \( v^3 \) , so erhält man folgende Ergebnisse:
| \( u_0 = \frac{5}{6} + i \cdot \frac{1}{6}\sqrt{3} \) | \( v_0 = -\frac{1}{6} + i \cdot \frac{1}{2}\sqrt{3} \) |
| \( u_1 = -\frac{2}{3} + i \cdot \frac{1}{3}\sqrt{3} \) | \( v_1 = -\frac{2}{3} - i \cdot \frac{1}{3}\sqrt{3} \) |
| \( u_2 = -\frac{1}{6} - i \cdot \frac{1}{2}\sqrt{3} \) | \( v_2 = \frac{5}{6} - i \cdot \frac{1}{6}\sqrt{3} \) |
Die Nebenbedingung \( 3uv + p = 0 \) wird von den Paaren \( (u_0|v_2) \) , \( (u_1|v_1) \) und \( (u_2|v_0) \) erfüllt.
Die drei Lösungen sind also:
\( z_1 = u_0 + v_2 = \frac{5}{3} \)
\( z_2 = u_1 + v_1 = -\frac{4}{3} \)
\( z_3 = u_2 + v_0 = -\frac{1}{3} \)
Mit \( x_i = z_i - \frac{1}{3}a \) ergibt sich:
\( x_1 = \frac{5}{3} - \frac{2}{3} = 1 \)
\( x_2 = -\frac{4}{3} - \frac{2}{3} = -2 \)
\( x_3 = -\frac{1}{3} - \frac{2}{3} = -1 \)
Anmerkung:
Kennt man ein gültiges Lösungspärchen \( (u|v) \) , zum Beispiel das Pärchen \( (u_0|v_2) \) im zuletzt betrachteten Fall, und somit eine erste Lösung \( z_1 \) , so kann man die beiden anderen Lösungen auch mit Hilfe der dritten Einheitswurzeln aus dieser ersten Lösung berechnen:
\( z_2 = u \cdot \varepsilon + v \cdot \varepsilon^2 \)
\( z_3 = u \cdot \varepsilon^2 + v \cdot \varepsilon \)
So weit das Beispiel zur Vorgehensweise ohne die Formeln für einzelne Fallunterscheidungen (1. Möglichkeit).
Es folgt nun die Behandlung der Fallunterscheidungen (2. Möglichkeit). Am Ende bekommt man Formeln, die für jeden möglichen Fall eindeutig die richtigen Ergebnisse liefern.
* * *
Fallunterscheidungen
In den Cardanischen Formeln entscheidet der Term unter der inneren Quadratwurzel darüber, ob die Werte für \( u^3 \) und \( v^3 \) reell oder komplex sind. Diese Diskriminante sei im Folgenden mit \( D \) bezeichnet, also:
\( D = (\frac{q}{2})^2 + (\frac{p}{3})^3 \) .
Die Cardanischen Formeln für \( u^3 \) bzw. \( v^3 \) haben dann folgende Gestalt:
\( u^3 = -\frac{q}{2} + \sqrt{D} \)
\( v^3 = -\frac{q}{2} - \sqrt{D} \)
In diesen beiden Gleichungen entscheidet das Vorzeichen der Diskriminante \( D \) , ob man für \( u^3 \) bzw. \( v^3 \) eine reelle oder eine komplexe Zahl erhält. Dadurch weichen die nachfolgenden Rechnungen voneinander ab.
Für \( D \ge 0 \) erhält man für \( u^3 \) und \( v^3 \) reelle Werte, für \( D < 0 \) komplexe Werte. Zur weiteren Berechnung der Lösungen \( u \) und \( v \) werden wir diese beiden Fälle gesondert behandeln.
Aus dem ersten Fall \( D \ge 0 \) werden jedoch zwei Spezialfälle extrahiert, so dass sich am Ende vier Fälle ergeben.
In den beiden Spezialfällen ist jeweils \( D = 0 \) , einmal mit \( q = 0 \) und einmal mit \( q \ne 0 \) .
Wir betrachten also folgende vier Fälle:
Fall 1: \( D = 0 \,\wedge\, q = 0 \) (Spezialfall)
Fall 2: \( D = 0 \,\wedge\, q \ne 0 \) (Spezialfall)
Fall 3: \( D > 0 \)
Fall 4: \( D < 0 \)
Zu jedem der vier Fälle wird nach der allgemeinen Lösung jeweils auch ein konkretes Beispiel berechnet.
* * *
1. Fall: \( D = 0 \,\wedge\, q = 0 \)
Allgemeine Rechnung:
Aus \( D = 0 \) und \( q = 0 \) folgt zwangsläufig auch \( p = 0 \) und somit \( u^3 = v^3 = 0 \) .
Aus \( u^3 = 0 \) und \( v^3 = 0 \) folgt \( u = 0 \) und \( v = 0 \) und somit auch \( z = 0 \) .
Die reduzierte Gleichung lautet in diesem Fall \( z^3 = 0 \) . Sie besitzt die dreifache Nullstelle \( z = 0 \) .
Durch Einsetzen in die erste Substitutionsgleichung \( x = z - \frac{1}{3}a \) erhält man die
einzige Lösung:
\( x = - \frac{1}{3}a \) .
Beispiel zu Fall 1: \( x^3 + 3x^2 + 3x + 1 = 0 \)
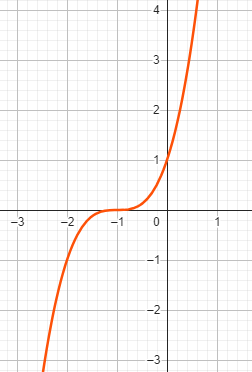
Im gegebenen Polynom haben wir die Koeffizienten \( a = 3 \) , \( b = 3 \) , \( c = 1 \) .
Berechnung von \( p \) und \( q \) :
\( p = b - \frac{1}{3}a^2 = 3 - \frac{1}{3} \cdot 3^2 = 0 \)
\( q = \frac{2}{27}a^3 - \frac{1}{3}ab + c = \frac{2}{27} \cdot 3^3 - \frac{1}{3} \cdot 3 \cdot 3 + 1 = 0 \)
Diskriminante: \( D = (\frac{q}{2})^2 + (\frac{p}{3})^3 = 0 \)
Lösung:
\( x = - \frac{1}{3}a = - \frac{1}{3} \cdot 3 = -1 \)
* * *
Ausblick
Die Fälle 2 und 3 kann man mit einer gemeinsamen Rechnung erledigen, die voraussetzt, dass \( D \ge 0 \) ist, der Fall 1 jedoch ausgeschlossen ist, also \( D \) und \( q \) nicht beide gleich null sind. Diese Voraussetzung kann man symbolisch so darstellen:
\( D \ge 0 \,\wedge\, \neg\, (D = 0 \,\wedge\, q = 0) \)
oder auch:
\( D \ge 0 \,\wedge\, (D \ne 0 \,\vee\, q \ne 0) \)
Es folgt deshalb die gemeinsame Rechnung für die Fälle 2 und 3.
Danach werden die Ergebnisse für den Fall 2 und den Fall 3 mit Beispielen dargestellt.
Anschließend wird der Fall 4 berechnet.
Eine Zusammenfassung der Ergebnisse aller vier Fälle schließt diese Herleitung der Lösungen ab.
* * *
Rechnung für den 2. und den 3. Fall: \( D \ge 0 \,\wedge\, (D \ne 0 \,\vee\, q \ne 0) \)
Die Diskriminante \( D \) ist positiv.
Der Fall \( D = 0 \) ist eingeschlossen, jedoch ist Fall 1 (siehe oben) ausgeschlossen:
\( D \) und \( q \) sind nicht beide gleich null.
Daraus folgt: \( u^3 \ne 0 \) .
Es gilt:
\( u^3 = -\frac{q}{2} + \sqrt{D} \)
\( u^3 \) ist eine reelle Zahl. Um die komplexen dritten Wurzeln aus dieser reellen Zahl zu ermitteln, wandeln wir sie zuerst in die Polarform um. Dabei sind zwei Fälle zu unterscheiden:
Fall 2/3 a: \( u^3 > 0 \)
Polarform: \( u^3 = |-\frac{q}{2} + \sqrt{D}\,| \cdot e^{i \cdot 0} \)
Fall 2/3 b: \( u^3 < 0 \)
Polarform: \( u^3 = |-\frac{q}{2} + \sqrt{D}\,| \cdot e^{i \cdot \pi} \)
Fall 2/3 a: \( u^3 > 0 \)
Für die dritten Wurzeln erhält man:
\( u_{1,2,3} = |-\frac{q}{2} + \sqrt{D}\,|^{\frac{1}{3}} \cdot e^{i \cdot \frac{2}{3}\pi k} \quad (k = 0,1,2) \)
Bei dem Faktor \( e^{i \cdot \frac{2}{3}\pi k} \) handelt es sich um die sog. ▸dritten Einheitswurzeln :
\( e^{i \cdot 0} = 1 \) ,
\( e^{i \cdot \frac{2}{3}\pi} = -\frac{1}{2} + i \cdot \frac{1}{2}\sqrt{3} \) ,
\( e^{i \cdot \frac{4}{3}\pi} = -\frac{1}{2} - i \cdot \frac{1}{2}\sqrt{3} \) ,
in Kurzschreibweise: \( 1, \varepsilon, \varepsilon^2 \) .
Der erste Faktor ist der Betrag \( r \) der komplexen Zahl:
\( r = |-\frac{q}{2} + \sqrt{D}\,|^{\frac{1}{3}} \) .
Somit können wir abkürzend schreiben:
\( u_{1,2,3} = r \cdot \varepsilon^k \quad (k = 0, 1, 2) \)
Anstatt nun genauso die dritten Wurzeln von \( v^3 \) zu berechnen und dann zu prüfen, welche drei der neun Kombinationen aus \( u_i \) und \( v_j \) die Gleichung \( (2) \) , also \( 3uv + p = 0 \) , erfüllen, berechnen wir die zugehörigen \( v_i \) durch Einsetzen in die Gleichung \( (2) \) . Damit erhalten wir sofort die richtige und eindeutige Zuordnung, also nur drei Lösungspaare \( (u_i|v_i) \) .
Aus \( 3uv + p = 0 \) folgt:
\( v = \frac{-\frac{p}{3}}{u} \) und somit
\( v_{1,2,3} = \frac{-\frac{p}{3}}{r \,\cdot\, \varepsilon^k} \quad (k = 0, 1, 2) \)
\( v_{1,2,3} = \frac{-\frac{p}{3}}{r} \cdot \varepsilon^{-k} \)
Damit die Hochzahlen der Einheitswurzeln positiv werden, multiplizieren wir mit dem Faktor \( 1 = \varepsilon^{3} \) . Dann ist \( \varepsilon^{-k} \cdot \varepsilon^{3} \,=\, \varepsilon^{-k+3} \,=\, \varepsilon^{3-k} \) .
Es folgt:
\( v_{1,2,3} = \frac{-\frac{p}{3}}{r} \cdot \varepsilon^{3-k} \)
\( v_{1,2,3} = \frac{-\frac{p}{3}}{\bigl|-\frac{q}{2} + \sqrt{D}\,\bigr|^{\frac{1}{3}}} \cdot \varepsilon^{3-k} \)
Wir erweitern mit \( |-\frac{q}{2} - \sqrt{D}\,|^{\frac{1}{3}} \) .
\( v_{1,2,3} = \frac{-\frac{p}{3} \color{rgb(253, 81, 8)}{\,\cdot\, \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}}}}{\bigl|-\frac{q}{2} + \sqrt{D}\,\bigr|^{\frac{1}{3}} \color{rgb(253, 81, 8)}{\,\cdot\, \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}}}} \cdot \varepsilon^{3-k} \)
\( v_{1,2,3} = \frac{-\frac{p}{3}}{\bigl| (-\frac{q}{2} + \sqrt{D}\,) \,\cdot\, (-\frac{q}{2} - \sqrt{D})\, \bigr| ^{\frac{1}{3}}} \,\cdot\, \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \cdot \varepsilon^{3-k} \)
\( v_{1,2,3} = \frac{-\frac{p}{3}}{\bigl| (\frac{q}{2})^2 - D \,\bigr| ^{\frac{1}{3}}} \,\cdot\, \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \cdot \varepsilon^{3-k} \)
Für \( D \) setzen wir den Term \( (\frac{q}{2})^2 + (\frac{p}{3})^3 \) ein:
\( v_{1,2,3} = \frac{-\frac{p}{3}}{\bigl| (\frac{q}{2})^2 - (\frac{q}{2})^2 - (\frac{p}{3})^3 \,\bigr| ^{\frac{1}{3}}} \,\cdot\, \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \cdot \varepsilon^{3-k} \)
\( v_{1,2,3} = \frac{-\frac{p}{3}}{\bigl|-(\frac{p}{3})^3 \,\bigr| ^{\frac{1}{3}}} \,\cdot\, \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \cdot \varepsilon^{3-k} \)
\( v_{1,2,3} = \frac{-\frac{p}{3}}{\bigl|-\frac{p}{3} \,\bigr|} \,\cdot\, \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \cdot \varepsilon^{3-k} \)
Der erste Bruch ergibt \( 1 \) für \( p < 0 \) und \( -1 \) für \( p > 0 \) . Deshalb kann man ihn durch die Signum-Funktion \( sgn(-p) \) ersetzen.
\( v_{1,2,3} = sgn(-p) \,\cdot\, \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \cdot \varepsilon^{3-k} \)
Die Zusammenfassung der Ergebnisse am Ende der Herleitungen wird noch effektiver sein, wenn wir zeigen, dass im Fall 2/3 a die Vorzeichen von \( -p \) und \( v^3 \) übereinstimmen. Deshalb dazu eine extra Betrachtung:
Beweis zu \( sgn(-p) = sgn(v^3) \) im Fall 2/3 a:
Es gilt: \( v^3 = -\frac{q}{2} - \sqrt{(\frac{q}{2})^2 + (\frac{p}{3})^3} \) .
Fall (i): \( q > 0 \)
Die Voraussetzungen für den Fall 2/3 a sind ja \( D \ge 0 \) und \( u^3 \ge 0 \) .
Die erste Voraussetzung \( D \ge 0 \) garantiert, dass die Wurzel reell ist. Die zweite Voraussetzung \( u^3 \ge 0 \) lautet ausgeschrieben:
\( -\frac{q}{2} + \sqrt{(\frac{q}{2})^2 + (\frac{p}{3})^3} \,\ge\, 0 \) .
Im Falle \( q > 0 \) folgt nun daraus \( p > 0 \) . Denn \( -\frac{q}{2} \) ist negativ und die (positive) Wurzel kann diese Negativität nur dann zum Positiven aufsummieren, wenn unter der Wurzel etwas größeres steht als \( (\frac{q}{2})^2 \) . Das heißt, \( p \) muss positiv sein.
Mit \( q > 0 \) und \( p > 0 \) folgt nun unweigerlich \( v^3 < 0 \) .
\( -p \) und \( v^3 \) sind also beide negativ, also \( sgn(-p) = sgn(v^3) \) .
Fall (ii): \( q < 0 \)
In diesem Fall kann \( p \) positiv oder negativ sein. Wir betrachten wieder den Term
\( v^3 = -\frac{q}{2} - \sqrt{(\frac{q}{2})^2 + (\frac{p}{3})^3} \) .
\( -\frac{q}{2} \) ist jetzt positiv.
Ist \( p \) positiv, so ist die Wurzel größer als \( -\frac{q}{2} \) und somit \( v^3 \) negativ.
D. h.: \( p > 0 \,\Rightarrow\, v^3 < 0 \) und somit \( sgn(-p) = sgn(v^3) \) .
Ist \( p \) negativ, so ist die Wurzel kleiner als \( -\frac{q}{2} \) und somit \( v^3 \) positiv.
D. h.: \( p < 0 \,\Rightarrow\, v^3 > 0 \) und somit \( sgn(-p) = sgn(v^3) \) .
An Stelle von \( sgn(-p) \) können wir also auch \( sgn(v^3) \) schreiben.
Damit sieht unsere letzte Ergebniszeile so aus:
\( v_{1,2,3} = sgn(v^3) \,\cdot\, \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \cdot \varepsilon^{3-k} \)
Mit
\( r_u = \bigl|-\frac{q}{2} + \sqrt{D}\,\bigr|^{\frac{1}{3}} \) ,
\( r_v = sgn(v^3) \,\cdot\, \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \) und
\( \varepsilon = -\frac{1}{2} + \frac{1}{2} \sqrt{3} \)
haben wir nun folgende Lösungen:
\( u_1 = r_u \)
\( u_2 = r_u \cdot \varepsilon \)
\( u_3 = r_u \cdot \varepsilon^{2} \)
und
\( v_1 = r_v \)
\( v_2 = r_v \cdot \varepsilon^{2} \)
\( v_3 = r_v \cdot \varepsilon \)
Aus \( z = u + v \) und \( x = z - \frac{1}{3}a \) ergibt sich:
\( x_1 = r_u \,+\, r_v - \frac{1}{3}a \)
\( x_2 = r_u \cdot \varepsilon \,+\, r_v \cdot \varepsilon^{2} - \frac{1}{3}a \)
\( x_3 = r_u \cdot \varepsilon^{2} \,+\, r_v \cdot \varepsilon - \frac{1}{3}a \)
Fall 2/3 b: \( u^3 < 0 \)
\( u^3 \) kann nur dann negativ sein, wenn \( p < 0 \) ist. Damit ist das Vorzeichen von \( p \) klar und wir benötigen die Signum-Funktion in diesem Fall nicht.
Da \( u^3 < 0 \) ist, enthält die Polarform von \( u^3 \) jetzt allerdings den Winkel \( \pi \) :
\( u^3 = |-\frac{q}{2} + \sqrt{D}\,| \cdot e^{i \pi} \)
Für die dritten Wurzeln erhält man:
\( u_{1,2,3} = |-\frac{q}{2} + \sqrt{D}\,|^{\frac{1}{3}} \cdot e^{i \cdot (\frac{1}{3}\pi + \frac{2}{3}\pi k)} \quad (k = 0,1,2) \)
Wir verwenden wieder die Abkürzung \( r = |-\frac{q}{2} + \sqrt{D}\,|^{\frac{1}{3}} \) :
\( u_{1,2,3} = r \cdot e^{i \cdot (\frac{1}{3}\pi + \frac{2}{3}\pi k)} \quad (k = 0,1,2) \)
Wir erhalten:\( u_1 = r \cdot e^{i \cdot \frac{1}{3}\pi} \)
\( u_2 = r \cdot e^{i \cdot \pi} \)
\( u_3 = r \cdot e^{i \cdot \frac{5}{3}\pi} \)
Um zu einer Schreibweise mit den dritten Einheitswurzeln zu gelangen, nutzen wir die Tatsache aus, dass sich das Vorzeichen der komplexen Zahl umdreht, wenn wir den Winkel der komplexen Zahl um \( \pi \) vergrößern oder verkleinern.
\( u_1 = - r \cdot e^{i \cdot \frac{4}{3}\pi} \) (\( \pi \) addiert)
\( u_2 = - r \cdot e^{i \cdot 0} \) (\( \pi \) subtrahiert)
\( u_3 = - r \cdot e^{i \cdot \frac{2}{3}\pi} \) (\( \pi \) subtrahiert)
Wieder können wir die Ergebnisse mit Hilfe der Einheitswurzeln darstellen:
\( u_1 = - r \cdot \varepsilon^2 \)
\( u_2 = - r \)
\( u_3 = - r \cdot \varepsilon \)
An dieser Stelle verändern wir die Reihenfolge der drei Lösungen:
\( u_1 = - r \)
\( u_2 = - r \cdot \varepsilon \)
\( u_3 = - r \cdot \varepsilon^2 \)
Auf diese Weise können wir die drei Gleichungen wie im Fall 2/3 a (siehe oben) zusammenfassen zu:
\( u_{1,2,3} = - r \cdot \varepsilon^k \quad (k = 0,1,2) \)
Die weitere Rechnung unterscheidet sich vom Fall 2/3 a nur dadurch, dass an Stelle von \( r \) jetzt \( -r \) steht und das Vorzeichen von \( p \) bekannt ist ( \( p \) ist negativ).
Es folgt:
\( v_{1,2,3} = \frac{-\frac{p}{3}}{-r} \cdot \varepsilon^{-k} \)
\( v_{1,2,3} = -\frac{-\frac{p}{3}}{r} \cdot \varepsilon^{3-k} \)
\( v_{1,2,3} = -\frac{-\frac{p}{3}}{\bigl|-\frac{q}{2} + \sqrt{D}\,\bigr|^{\frac{1}{3}}} \cdot \varepsilon^{3-k} \)
Nach der Erweiterung mit \( |-\frac{q}{2} - \sqrt{D}\,|^{\frac{1}{3}} \) und weiterer Vereinfachung (vergleiche Fall 2/3 a) erhalten wir:
\( v_{1,2,3} = -\frac{-\frac{p}{3}}{\bigl|-\frac{p}{3} \,\bigr|} \,\cdot\, \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \cdot \varepsilon^{3-k} \)
Da wir wissen, dass \( p < 0 \) ist, brauchen wir für den ersten Bruch nicht mehr die Signum-Funktion einzusetzen. Der Zähler ist positv, der Nenner auch, also ist der Bruch gleich \( 1 \) .
\( v_{1,2,3} = -\bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \cdot \varepsilon^{3-k} \)
Mit \( r_u = \bigl|-\frac{q}{2} + \sqrt{D}\,\bigr|^{\frac{1}{3}} \) und \( r_v = \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \) und \( \varepsilon = -\frac{1}{2} + \frac{1}{2} \sqrt{3} \) haben wir nun folgende Lösungen:
\( u_1 = - r_u \)
\( u_2 = - r_u \cdot \varepsilon \)
\( u_3 = - r_u \cdot \varepsilon^{2} \)
und
\( v_1 = - r_v \)
\( v_2 = - r_v \cdot \varepsilon^{2} \)
\( v_3 = - r_v \cdot \varepsilon \)
Aus \( z = u + v \) und \( x = z - \frac{1}{3}a \) ergibt sich dann:
\( x_1 = - r_u \,-\, r_v - \frac{1}{3}a \)
\( x_2 = - r_u \cdot \varepsilon \,-\, r_v \cdot \varepsilon^{2} - \frac{1}{3}a \)
\( x_3 = - r_u \cdot \varepsilon^{2} \,-\, r_v \cdot \varepsilon - \frac{1}{3}a \)
Einheitliche Lösung für die Fälle 2/3 a und 2/3 b:
Wenn man die Lösungen von Fall 2/3 a und Fall 2/3 b vergleicht, stellt man fest, dass man mit Hilfe der Signum-Funktion für beide Fälle eine einheitliche Schreibweise angeben kann.
Im Fall 2/3 a kann man für \( r_u \) auch \( sgn(u^3) \cdot r_u \) schreiben, weil laut Voraussetzung \( u^3 > 0 \) gilt.
Im Fall 2/3 b kann man für \( -r_u \) ebenfalls \( sgn(u^3) \cdot r_u \) schreiben, weil laut Voraussetzung \( u^3 < 0 \) gilt.
Und für \( -r_v \) kann man \( sgn(v^3) \cdot r_v \) schreiben, weil aus \( u^3 < 0 \) in diesem Fall \( v^3 < 0 \) folgt.
Letzeres kann man z. B. dadurch nachweisen, dass man die für \( v_{1,2,3} \) gefundenen Lösungen mit \( 3 \) potenziert.
Aus der Gleichung
\( v_{1,2,3} = -\bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \cdot \varepsilon^{3-k} \)
ergibt sich:
\( v^3 = (v_{1,2,3})^3 = -\bigl|-\frac{q}{2} - \sqrt{D}\,\bigr| \,< 0 \)
Die dritte Einheitswurzel am Ende des Terms potenziert mit \( 3 \) ergibt (für jedes \( k \) ) den Wert \( 1 \) .
Setzen wir
\( r_u = sgn(u^3) \,\cdot\, \bigl|-\frac{q}{2} + \sqrt{D}\,\bigr|^{\frac{1}{3}} \) und
\( r_v = sgn(v^3) \,\cdot\, \bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|^{\frac{1}{3}} \) ,
so erhalten wir für beide Fälle die Lösungen:
\( x_1 = r_u \,+\, r_v - \frac{1}{3}a \)
\( x_2 = r_u \cdot \varepsilon \,+\, r_v \cdot \varepsilon^{2} - \frac{1}{3}a \)
\( x_3 = r_u \cdot \varepsilon^{2} \,+\, r_v \cdot \varepsilon - \frac{1}{3}a \)
Die erste Lösung \( x_1 \) ist reell.
Für \( x_2 \) und \( x_3 \) erhalten wir komplexe Zahlen.
Real- und Imaginärteil der komplexen Lösungen \( x_2 \) und \( x_3 \) :
In einem weiteren Rechenschritt ermitteln wir Formeln für den Real- und Imaginärteil der beiden Lösungen \( x_2 \) und \( x_3 \) . Dazu setzen wir für \( \varepsilon \) und \( \varepsilon^2 \) die entsprechenden Terme ein:
\( x_2 = r_u \cdot (-\frac{1}{2} + i \cdot \frac{1}{2} \sqrt{3}) \,+\, r_v \cdot (-\frac{1}{2} - i \cdot \frac{1}{2} \sqrt{3}) - \frac{1}{3}a \)
\( x_2 = -\frac{1}{2} r_u + i \cdot \frac{1}{2} \sqrt{3}\,r_u - \frac{1}{2} r_v - i \cdot \frac{1}{2} \sqrt{3}\,r_v - \frac{1}{3}a \)
\( x_2 = \underbrace{-\frac{1}{2} (r_u + r_v) - \frac{1}{3}a}_{\text{Realteil}} \,+\, i \cdot \underbrace{\frac{1}{2} \sqrt{3}\,(r_u - r_v)}_{\text{Imaginärteil}} \)
Dieselbe Rechnung für \( x_3 \) :
\( x_3 = r_u \cdot (-\frac{1}{2} - i \cdot \frac{1}{2} \sqrt{3}) \,+\, r_v \cdot (-\frac{1}{2} + i \cdot \frac{1}{2} \sqrt{3}) - \frac{1}{3}a \)
\( x_3 = -\frac{1}{2} r_u - i \cdot \frac{1}{2} \sqrt{3}\,r_u - \frac{1}{2} r_v + i \cdot \frac{1}{2} \sqrt{3}\,r_v - \frac{1}{3}a \)
\( x_3 = \underbrace{-\frac{1}{2} (r_u + r_v) - \frac{1}{3}a}_{\text{Realteil}} \,-\, i \cdot \underbrace{\frac{1}{2} \sqrt{3}\,(r_u - r_v)}_{\text{Imaginärteil}} \)
Wir sehen, dass \( x_2 \) und \( x_3 \) konjugiert komplex zueinander sind.
Für \( x_3 \) ist also keine zusätzliche Rechnung mehr erforderlich.
Nebenbemerkung:
Nutzt man weitergehende Kenntnisse aus, so kann man sich einen Großteil dieser Rechnungen ersparen. Zum Beispiel kann man verwenden, dass es im Komplexen für die dritten Wurzeln immer drei Lösungen gibt, von denen zwei konjugiert komplex zueinander sind, und dass es genügt, eine der drei dritten Wurzeln zu wissen, weil sich die beiden anderen aus dieser einen durch Multiplikation mit \( \varepsilon \) und \( \varepsilon^2 \) ergeben.
Mein Ziel war es allerdings, hier eine ausführliche und möglichst lückenlose Berechnung aufzuzeigen, die jemand mit Schulwissen plus Basiswissen über komplexe Zahlen nachvollziehen kann.
Die reelle Lösung \( x_1 \) lautet in ausführlicher Form und unter Verwendung des Wurzelsymbols:
\( x_1 = sgn(u^3) \cdot \sqrt[3]{\bigl|-\frac{q}{2} + \sqrt{D}\,\bigr|} \,+\, sgn(v^3) \cdot \sqrt[3]{\bigl|-\frac{q}{2} - \sqrt{D}\,\bigr|} \,-\, \frac{1}{3}a \)
Sie wird gelegentlich auch ohne die Signumfunktion und die Betragsstriche unter der Wurzel publiziert:
\( x_1 = \sqrt[3]{-\frac{q}{2} + \sqrt{D}} \,+\, \sqrt[3]{-\frac{q}{2} - \sqrt{D}} \,-\, \frac{1}{3}a \)
oder in der ausführlichen Form:
\( x_1 = \sqrt[3]{-\frac{q}{2} + \sqrt{(\frac{q}{2})^2 + (\frac{p}{3})^3}} \,+\, \sqrt[3]{-\frac{q}{2} - \sqrt{(\frac{q}{2})^2 + (\frac{p}{3})^3}} \,-\, \frac{1}{3}a \)
Diese Schreibweise ignoriert die mathematische Norm DIN 1302, die allerdings in diesem speziellen Punkt selbst unter Mathematikern bis heute umstritten ist. Nach dieser Norm existiert die Wurzel aus einer negativen Zahl im Reellen nicht. Auch die Taschenrechner ignorieren diese Norm, denn sie ziehen problemlos die dritte Wurzel auch aus negativen Zahlen.
Wir sind nun am Ende der für die Fälle 2 und 3 gemeinsamen Rechnung angekommen. Im Spezialfall 2 ist \( D = 0 \) . In diesem Fall lassen sich die Formeln für das Endergebnis noch weiter vereinfachen. Nach dieser Vereinfachung der Formeln für den Fall 2 folgt dann die Formulierung der Formeln für den Fall 3 (\( D > 0 \)).
* * *
2. Fall: \( D = 0 \,\wedge\, q \ne 0 \)
In diesem besonderen Fall gilt:
\( u^3 = v^3 = -\frac{q}{2} \)
\( r = r_u = r_v = sgn(-\frac{q}{2}) \cdot \bigl|-\frac{q}{2}\bigr|^{\frac{1}{3}} \)
\( r = -sgn(q) \cdot \bigl|\frac{q}{2}\bigr|^{\frac{1}{3}} \)
Die Signum-Funktion und die dritte Wurzel kann man vermeiden, wenn man die Gleichheit
\( -sgn(q) \cdot \bigl|\frac{q}{2}\bigr|^{\frac{1}{3}} = \frac{3\,q}{2\,p} \) ausnutzt.
Beweis zu \( -sgn(q) \cdot \bigl|\frac{q}{2}\bigr|^{\frac{1}{3}} = \frac{3\,q}{2\,p} \)
Wegen \( D = 0 \) gilt:
\( (\frac{q}{2})^2 = -(\frac{p}{3})^3 \)
Die Gleichung wird mit \( \frac{q}{2} \) multipliziert:
\( (\frac{q}{2})^2 \cdot \frac{q}{2} = -(\frac{p}{3})^3 \cdot \frac{q}{2} \)
\( (\frac{q}{2})^3 = (-\frac{p}{3})^3 \cdot \frac{q}{2} \)
Zu beachten: Wegen \( D = 0 \) ist \( p < 0 \) und somit \( \bigl(-\frac{p}{3}\bigr)^3 \) eine positive Zahl!
Wenn wir jetzt auf der linken Seite \( \frac{q}{2} \) haben wollen, beginnt sie wieder, die ewige Diskussion: "Darf ich aus einer negativen Zahl die dritte Wurzel ziehen?"
Denn im Falle \( q < 0 \) steht auf beiden Seiten eine negative Zahl!
In der mathematischen Norm DIN 1302 ist klar geregelt, dass in der Menge der reellen Zahlen die Wurzel aus einer negativen Zahl nicht definiert ist. Im Sinne dieser Regelung hat die Gleichung \( x^3 = a \) nicht die Lösung \( x = \sqrt[3]{a} \) , sondern die Lösung \( x = sgn(a) \cdot \sqrt[3]{|a|} \) .
Wir ziehen an dieser Stelle nicht die dritte Wurzel, sondern wir nutzen die Tatsache aus, dass im Reellen gilt: \( a^3 = b^3 \,\Leftrightarrow\, a = b \) .
(Diese Äquivalenz gilt übrigens nicht für komplexe Zahlen.)
Es folgt:
\( \frac{q}{2} = -\frac{p}{3} \cdot sgn(q) \cdot \bigl|\frac{q}{2}\bigr|^{\frac{1}{3}} \)
Division durch \( \frac{p}{3} \) ergibt:
\( \frac{3\,q}{2\,p} = -sgn(q) \cdot \bigl|\frac{q}{2}\bigr|^{\frac{1}{3}} \)
(Wenn \( q \) positiv ist, steht auf der linken Seite eine negative Zahl, weil \( p \) in dem hier betrachteten 2. Fall negativ ist!)
Für \( r \) können wir nun auch schreiben:
\( r = \frac{3\,q}{2\,p} \)
Durch Einsetzen in die Lösungsformeln für den 2. und 3. Fall ergibt sich:
\( x_1 = r + r - \frac{1}{3}a \)
\( x_1 = 2\,r - \frac{1}{3}a \)
\( x_2 = r \cdot \varepsilon \,+\, r \cdot \varepsilon^2 - \frac{1}{3}a \)
\( x_2 = r \cdot (\varepsilon + \varepsilon^2) - \frac{1}{3}a \)
Da die Einheitswurzeln \( \varepsilon \) und \( \varepsilon^2 \) konjugiert komplex zueinander sind, fallen die Imaginärteile bei der Summe weg:
\( \varepsilon + \varepsilon^2 = -\frac{1}{2} + i \cdot \frac{1}{2} \sqrt{3} - \frac{1}{2} - i \cdot \frac{1}{2} \sqrt{3} = -1 \)
\( x_2 = -r - \frac{1}{3}a \)
\( x_3 = r \cdot \varepsilon^2 \,+\, r \cdot \varepsilon - \frac{1}{3}a \)
\( x_3 = r \cdot (\varepsilon^2 + \varepsilon) - \frac{1}{3}a \)
Mit \( \varepsilon^2 + \varepsilon = -1 \) folgt:
\( x_3 = -r - \frac{1}{3}a \)
Für \( x_2 \) und \( x_3 \) erhalten wir denselben (reellen) Wert. Es handelt sich um eine doppelte Nullstelle.
Lösungen für den 2. Fall:
\( x_1 = \frac{3\,q}{p} - \frac{1}{3}a \)
\( x_{2,3} = -\frac{3\,q}{2\,p} - \frac{1}{3}a \)
Beispiel zu Fall 2: \( x^3 + 9x^2 + 24x + 20 = 0 \)
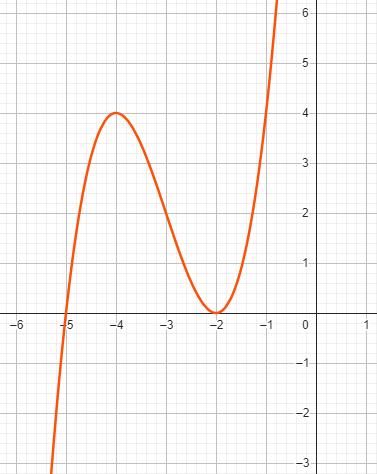
Im gegebenen Polynom haben wir die Koeffizienten \( a = 9 \) , \( b = 24 \) , \( c = 20 \) .
Berechnung von \( p \) und \( q \) :
\( p = b - \frac{1}{3}a^2 \)
\( p = 24 - \frac{1}{3} \cdot 9^2 \)
\( p = -3 \)
\( q = \frac{2}{27}a^3 - \frac{1}{3}ab + c \)
\( q = \frac{2}{27} \cdot 9^3 - \frac{1}{3} \cdot 9 \cdot 24 + 20 \)
\( q = 2 \)
Diskriminante \( D \) :
\( D = (\frac{q}{2})^2 + (\frac{p}{3})^3 \)
\( D = (\frac{2}{2})^2 + (\frac{-3}{3})^3 \)
\( D = 0 \)
Aus den Lösungsformeln für den 2. Fall ergibt sich:
\( x_1 = \frac{3\,q}{p} - \frac{1}{3}a \)
\( x_1 = \frac{3 \,\cdot\, 2}{-3} -\frac{1}{3} \cdot 9 \)
\( x_1 = -5 \)
\( x_{2,3} = -\frac{3\,q}{2\,p} - \frac{1}{3}a \)
\( x_{2,3} = -\frac{3 \,\cdot\, 2}{2 \,\cdot\, (-3)} -\frac{1}{3} \cdot 9 \)
\( x_{2,3} = -2 \)
* * *
3. Fall: \( D > 0 \)
Die allgemeine Lösung wurde weiter oben in der gemeinsamen Rechnung für den 2. und den 3. Fall bereits hergeleitet. Sie sei an dieser Stelle nochmals genannt.
Lösungen für den 3. Fall:
Mit
\( u^3 = -\frac{q}{2} + \sqrt{D} \)
\( v^3 = -\frac{q}{2} - \sqrt{D} \)
\( r_u = sgn(u^3) \,\cdot\, \bigl|u^3\bigr|^{\frac{1}{3}} \)
\( r_v = sgn(v^3) \,\cdot\, \bigl|v^3\bigr|^{\frac{1}{3}} \)
gilt:
\( x_1 = r_u \,+\, r_v - \frac{1}{3}a \)
\( x_2 = \underbrace{-\frac{1}{2} (r_u + r_v) - \frac{1}{3}a}_{\text{Realteil}} \,+\, i \cdot \underbrace{\frac{1}{2} \sqrt{3}\,(r_u - r_v)}_{\text{Imaginärteil}} \)
\( x_3 = \overline{x_2} \)
Beispiel zu Fall 3: \( x^3 + 6x^2 + 9x - 2 = 0 \)
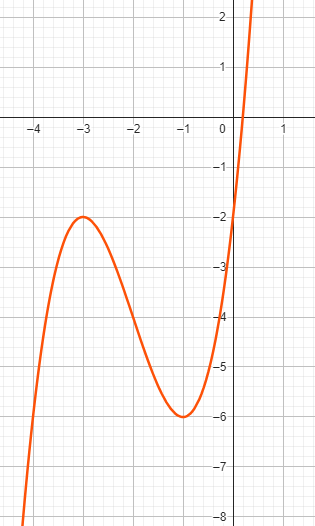
Im gegebenen Polynom haben wir die Koeffizienten \( a = 6 \) , \( b = 9 \) , \( c = -2 \) .
Berechnung von \( p \) und \( q \) :
\( p = b - \frac{1}{3}a^2 \)
\( p = 9 - \frac{1}{3} \cdot 6^2 \)
\( p = -3 \)
\( q = \frac{2}{27}a^3 - \frac{1}{3}ab + c \)
\( q = \frac{2}{27} \cdot 6^3 - \frac{1}{3} \cdot 6 \cdot 9 - 2 \)
\( q = -4 \)
Diskriminante \( D \) :
\( D = (\frac{q}{2})^2 + (\frac{p}{3})^3 \)
\( D = (\frac{-4}{2})^2 + (\frac{-3}{3})^3 \)
\( D = 3 \)
Wir berechnen:
\( u^3 = -\frac{q}{2} + \sqrt{D} \)
\( u^3 = -\frac{-4}{2} + \sqrt{3} \)
\( u^3 = 2 + \sqrt{3} \)
\( v^3 = 2 - \sqrt{3} \)
Mit \( sgn(u^3) = 1 \) und \( sgn(v^3) = 1 \) folgt:
\( r_u = \Bigl|\,2 + \sqrt{3}\,\Bigr|^{\frac{1}{3}} \,\approx 1,5511 \)
\( r_v = \Bigl|\,2 - \sqrt{3}\,\Bigr|^{\frac{1}{3}} \,\approx 0,6447 \)
(Die Werte für \( r_u \) und \( r_v \) werden im Speicher hinterlegt.)
Wir setzen in die Lösungsformeln für den 3. Fall ein:
\( x_1 = r_u \,+\, r_v - 2 \)
\( x_1 \approx 0,1958 \) (reelle Nullstelle)
\( x_2 = \underbrace{-\frac{1}{2} (r_u + r_v) - 2}_{\text{Realteil}} \,+\, i \cdot \underbrace{\frac{1}{2} \sqrt{3}\, (r_u - r_v)}_{\text{Imgainärteil}} \)
\( x_2 \approx -3,0979 + i \cdot 0,7850 \)
\( x_3 = \overline{x_2} \)
\( x_3 \approx -3,0979 - i \cdot 0,7850 \)
* * *
4. Fall: \( D < 0 \)
Dieser Fall ist als "casus irreducibilis" (nicht zurückführbarer Fall) in die Geschichte eingegangen. Am Anfang des 16. Jahrhunderts war es nicht möglich, die reellen Lösungen mit Hilfe von Wurzeltermen zu berechnen. Man konnte die Lösungen sozusagen nicht auf Wurzelterme zurückführen.
Erst durch die Entdeckung der imaginären Zahlen im Laufe des 16. Jahrhunderts gelang es Gerolamo Cardano und anderen Mathematikern, auch diese Lösungen zu berechnen.
Der Term für \( u^3 \) lautet:
\( u^3 = -\frac{q}{2} + \sqrt{D} \) .
Bei negativem \( D \) war die Wurzel Anfang des 16. Jahrhunderts nicht definiert. Es existierte also keine Zahl, die gleich \( u^3 \) wäre. Die Mathematiker damals wussten, dass es trotzdem drei reelle Lösungen gibt. Deshalb war dieser Fall damals höchst mysteriös.
Die Wurzel aus einer negativen Zahl \( D \) hat in der Menge der komplexen Zahlen zwei verschiedene Lösungen:
\( \sqrt{D}_{(1)} = \hspace{0.8em} i \cdot \sqrt{|D|} \)
\( \sqrt{D}_{(2)} = - i \cdot \sqrt{|D|} \) .
Mit Hilfe der komplexen Zahlen können wir daher schreiben:
\( u^3 = -\frac{q}{2} \pm i \cdot \sqrt{|D|} \) .
Für \( v^3 \) gilt dieselbe Gleichung. Wir bekämen sechs Lösungen (dritte Wurzeln) für \( u \) und sechs Lösungen (dritte Wurzeln) für \( v \) . Jedes Lösungspaar \( (u|v) \) würde aber doppelt vorkommen. Die Variablen \( u \) und \( v \) tauschen wiederum nur ihre Rollen. Wir können uns also bei \( u^3 \) auf das Pluszeichen beschränken. Die Wurzeln, die beim Minuszeichen herauskommen, können dann als die Wurzeln von \( v^3 \) angesehen werden.
Es folgt:
\( u^3 = -\frac{q}{2} + i \cdot \sqrt{|D|} \) .
Zur Berechnung der dritten Wurzeln wandeln wir \( u^3 \) in die Polarform um.
1. Berechnung des Betrags der komplexen Zahl \( u^3 \) :
\( |u^3| = \sqrt{(\frac{q}{2})^2 + |D|} \)
Da \( D < 0 \) ist, gilt: \( |D| = -D \) .
\( |u^3| = \sqrt{(\frac{q}{2})^2 - D} \)
Mit \( D = (\frac{q}{2})^2 + (\frac{p}{3})^3 \) folgt:
\( |u^3| = \sqrt{(\frac{q}{2})^2 - (\frac{q}{2})^2 - (\frac{p}{3})^3} \)
\( |u^3| = \sqrt{ - (\frac{p}{3})^3} \)
\( |u^3| = \sqrt{(-\frac{p}{3})^3} \)
Man beachte, dass in diesem 4. Fall immer \( p < 0 \) ist, weil \( D \) sonst nicht kleiner als Null werden könnte. Unter dem Wurzelzeichen steht also eine positive Zahl!
2. Berechnung des Winkels \( \delta \) der komplexen Zahl \( u^3 \) :
Da \( u^3 \) einen positiven Imaginärteil hat, liegt diese komplexe Zahl im ersten oder zweiten Quadranten der Gaußschen Zahlenebene. Daher gilt:
\( \delta = arccos \Bigl[\frac{-\frac{q}{2}}{|u^3|}\Bigr] \)
\( \delta = arccos \Biggl[\frac{-\frac{q}{2}}{\sqrt{\bigl(-\frac{p}{3}\bigr)^3}}\Biggr] \)
\( \delta = arccos \Bigl[-\frac{q}{2} \cdot \sqrt{\bigl(-\frac{3}{p}\bigr)^3}\,\Bigr] \)
Mit diesem Winkel \( \delta \) erhalten wir als Polarform von \( u^3 \) :
\( u^3 = \sqrt{(-\frac{p}{3})^3} \cdot e^{i \,\delta} \) .
3. Berechnung der dritten Wurzeln \( u_i \) der komplexen Zahl \( u^3 \) :
Die dritten Wurzeln von \( u^3 \) sind:
\( u_{1,2,3} = \Bigl(\sqrt{(-\frac{p}{3})^3}\,\Bigr)^\frac{1}{3} \cdot e^{i \cdot (\frac{1}{3}\delta + \frac{2}{3}\pi k)} \quad (k=0,1,2) \)
Wir vereinfachen den Term für den Betrag (die Zahl unter der Wurzel ist positiv!) und setzen außerdem \( \varphi := \frac{1}{3} \delta \) .
\( u_{1,2,3} = \sqrt{ - \frac{p}{3}} \cdot e^{i \cdot (\varphi + \frac{2}{3}\pi k)} \quad (k=0,1,2) \)
4. Berechnung der komplexen Zahlen \( v_i \) :
Die Berechnung der komplexen Zahlen \( v_{1,2,3} \) geschieht auch hier wieder über die Gleichung \( 3uv = -p \) :
\( v_{1,2,3} = \frac{-\frac{p}{3}}{u_{1,2,3}} \)
\( v_{1,2,3} = \frac{-\frac{p}{3}}{\sqrt{ - \frac{p}{3}} \,\cdot\, e^{i \cdot (\varphi + \frac{2}{3}\pi k)}} \quad (k=0,1,2) \)
\( v_{1,2,3} = \frac{-\frac{p}{3}}{\sqrt{ - \frac{p}{3}}} \cdot e^{-i \cdot (\varphi + \frac{2}{3}\pi k)} \quad (k=0,1,2) \)
An dieser Stelle die Erinnerung, dass \( -\frac{p}{3} \) wegen \( p < 0 \) eine positive Zahl ist und dass \( \frac{a}{\sqrt{a}} = \sqrt{a} \) ist:
\( v_{1,2,3} = \sqrt{-\frac{p}{3}} \cdot e^{-i \cdot (\varphi + \frac{2}{3}\pi k)} \quad (k=0,1,2) \)
Die \( v_i \) unterscheiden sich von den \( u_i \) nur im Vorzeichen des Winkels. Komplexe Zahlen, die sich nur im Vorzeichen des Winkels unterscheiden, sind zueinander konjugiert komplex.
Denn mit \( cos (-\,\alpha) = cos \,\alpha \) und \( sin (-\,\alpha) = - sin \,\alpha \) folgt:
\( r \cdot e^{i \alpha} = r \cdot (cos \,\alpha + i \cdot sin \,\alpha) \)
und
\( r \cdot e^{-i \alpha} = r \cdot (cos (-\alpha) + i \cdot sin (-\alpha)) \\
= r \cdot (cos \,\alpha - i \cdot sin \,\alpha) \)
Wir haben somit:
\( v_1 = \overline{u_1} \) , \( v_2 = \overline{u_2} \) und \( v_3 = \overline{u_3} \) .
Wenn wir nun zur Berechnung der Endergebnisse \( x_{1,2,3} \) die Summen \( u_i + v_i \) bilden, fallen die Imaginärteile weg und wir erhalten das Doppelte der jeweiligen Realteile:
\( x_i = 2 \cdot Re(u_i) - \frac{1}{3}a \) .
Wir erhalten also drei reelle Lösungen!
Lösungen für den 4. Fall:
Mit
\( \varphi = \frac{1}{3} \cdot arccos \Bigl[-\frac{q}{2} \cdot \sqrt{\bigl(-\frac{3}{p}\bigr)^3}\,\Bigr] \)
gilt:
\( x_1 = 2 \cdot \sqrt{ - \frac{p}{3}} \cdot cos\,\varphi - \frac{1}{3}a \)
\( x_2 = 2 \cdot \sqrt{ - \frac{p}{3}} \cdot cos(\varphi + \frac{2}{3}\pi) - \frac{1}{3}a \)
\( x_3 = 2 \cdot \sqrt{ - \frac{p}{3}} \cdot cos(\varphi + \frac{4}{3}\pi) - \frac{1}{3}a \)
Beispiel zu Fall 4: \( x^3 - x^2 - 2x + 1 = 0 \)
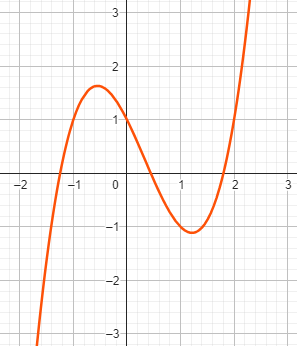
Im gegebenen Polynom haben wir die Koeffizienten \( a = -1 \) , \( b = -2 \) , \( c = 1 \) .
Berechnung von \( p \) und \( q \) :
\( p = b - \frac{1}{3}a^2 \)
\( p = -2 - \frac{1}{3} \cdot (-1)^2 \)
\( p = -\frac{7}{3} \)
\( q = \frac{2}{27}a^3 - \frac{1}{3}ab + c \)
\( q = \frac{2}{27} \cdot (-1)^3 - \frac{1}{3} \cdot (-1) \cdot (-2) + 1 \)
\( q = \frac{7}{27} \)
Diskriminante \( D \) :
\( D = (\frac{q}{2})^2 + (\frac{p}{3})^3 \)
\( D = (\frac{7}{54})^2 + (-\frac{7}{9})^3 \)
\( D = -\frac{49}{108} \)
Einsetzen in die Lösungsformeln für den 4. Fall:
\( \varphi = \frac{1}{3} \cdot arccos \Biggl[-\frac{\frac{7}{27}}{2} \cdot \sqrt{\Bigl(-\frac{3}{-\frac{7}{3}}\Bigr)^3}\,\Biggr] \)
\( \varphi = \frac{1}{3} \cdot arccos \Bigl[-\frac{7}{54} \cdot \sqrt{\bigl(\frac{9}{7}\bigr)^3}\,\Bigr] \)
\( \varphi \approx 0.58697 \)
\( x_1 = 2 \cdot \sqrt{\frac{7}{9}} \cdot cos\,\varphi + \frac{1}{3} \)
\( x_2 = 2 \cdot \sqrt{\frac{7}{9}} \cdot cos(\varphi + \frac{2}{3}\pi) + \frac{1}{3} \)
\( x_3 = 2 \cdot \sqrt{\frac{7}{9}} \cdot cos(\varphi + \frac{4}{3}\pi) + \frac{1}{3} \)
\( x_1 \approx 1,8019 \)
\( x_2 \approx -1,2470 \)
\( x_3 \approx 0,4450 \)
* * *
Zusammenfassung der Ergebnisse aller vier Fälle
Die Nullstellen eines Polynoms dritten Grades sollen bestimmt werden:
\( x^3+a\,x^2+b\,x+c=0 \)
Berechnung von \( p \) , \( q \) und \( D \) :
\( p = b - \frac{1}{3}a^2 \)
\( q = \frac{2}{27}a^3 - \frac{1}{3}ab + c \) .
\( D = (\frac{q}{2})^2 + (\frac{p}{3})^3 \)
Anhand der Werte für \( p \) , \( q \) und \( D \) ergeben sich vier Fälle:
1. Fall: \( D = 0 \,\wedge\, q = 0 \) :
\( x = - \frac{1}{3}a \) .
2. Fall: \( D = 0 \,\wedge\, q \ne 0 \) :
\( x_1 = \frac{3\,q}{p} - \frac{1}{3}a \)
\( x_{2,3} = -\frac{3\,q}{2\,p} - \frac{1}{3}a \)
3. Fall: \( D > 0 \) :
Mit
\( D = (\frac{q}{2})^2 + (\frac{p}{3})^3 \)
\( u^3 = -\frac{q}{2} + \sqrt{D} \)
\( v^3 = -\frac{q}{2} - \sqrt{D} \)
\( r_u = sgn(u^3) \,\cdot\, \bigl|u^3\bigr|^{\frac{1}{3}} \)
\( r_v = sgn(v^3) \,\cdot\, \bigl|v^3\bigr|^{\frac{1}{3}} \)
gilt:
\( x_1 = r_u \,+\, r_v - \frac{1}{3}a \)
\( x_2 = \underbrace{-\frac{1}{2} (r_u + r_v) - \frac{1}{3}a}_{\text{Realteil}} \,+\, i \cdot \underbrace{\frac{1}{2} \sqrt{3}\,(r_u - r_v)}_{\text{Imaginärteil}} \)
\( x_3 = \overline{x_2} \)
4. Fall: \( D < 0 \) :
Mit
\( \varphi = \frac{1}{3} \cdot arccos \Bigl[-\frac{q}{2} \cdot \sqrt{\bigl(-\frac{3}{p}\bigr)^3}\,\Bigr] \)
gilt:
\( x_1 = 2 \cdot \sqrt{ - \frac{p}{3}} \cdot cos\,\varphi - \frac{1}{3}a \)
\( x_2 = 2 \cdot \sqrt{ - \frac{p}{3}} \cdot cos(\varphi + \frac{2}{3}\pi) - \frac{1}{3}a \)
\( x_3 = 2 \cdot \sqrt{ - \frac{p}{3}} \cdot cos(\varphi + \frac{4}{3}\pi) - \frac{1}{3}a \)