Seite zuletzt aktualisiert: 05.07.2023
Aufgabenstellung
Gegeben sind zwei parallele Geraden g und h im \(\, \mathbb{R}^3 \).
Die Gerade g ist durch den Stützpunkt \(\, P \,\) und den Richtungsvektor \(\, \vec u \,\) festgelegt,
die Gerade h durch den Stützpunkt \(\, Q \,\) und den gleichen Richtungsvektor \(\, \vec u \,\).
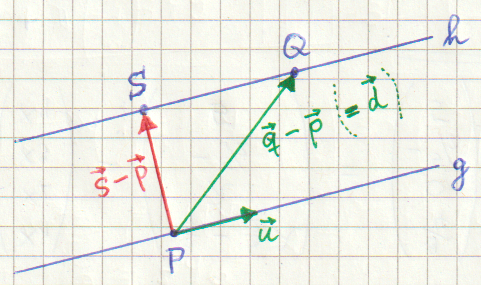
Es soll der (kürzeste) Abstand \(\, a \,\) dieser beiden Geraden berechnet werden.
* * *
Lösungsidee
Wir suchen auf der Geraden h einen Punkt \(\, S \,\) mit der Eigenschaft, dass der Vektor \(\, \overrightarrow{P S} \,\) orthogonal zum Vektor \(\, \vec u \,\) ist. Die Länge des Vektors \(\, \overrightarrow{P S} \,\) ist dann der gesuchte Abstand \(\, a \,\).
Statt diese Schritte mit den gegebenen Zahlen einzeln durchzuführen, soll im Folgenden eine allgemeine Formel hergeleitet werden.
Gegebene Größen: \(\, P \,\), \(\, Q \,\), \(\, \vec u \,\)
Gesucht: \(\, a \,\)
* * *
Herleitung
Wir haben zwei Schritte vor uns:
- Die Bestimmung des Punktes \(\, S \,\)
- Die Berechnung der Länge \(\, |\overrightarrow{P S}| \,\)
Schritt 1: Berechnung des Punktes \(\, S \,\)
Für den Punkt \(\, S \,\) gilt: \(\, \vec s = \vec q + \lambda \cdot \vec u \,\). (1)
Wenn die Vektoren \(\, \overrightarrow{P S} \,\) und \(\, \vec u \,\) orthogonal zueinander sein sollen, dann muss das Skalarprodukt beider Vektoren gleich null sein.
Ein passendes \(\, \lambda \,\) kann daher mit der Gleichung \(\, (\vec s - \vec p) \cdot \vec u = 0 \,\) bestimmt werden.
Für \(\, \vec s \,\) setzen wir den Ausdruck \(\, \vec q + \lambda \cdot \vec u \,\) ein und erhalten die Gleichung
\(\, (\vec q + \lambda \cdot \vec u - \vec p) \cdot \vec u = 0 \,\)
Um die Terme möglichst übersichtlich zu machen, verwenden wir folgende kürzere Schreibweisen:
\(\, \vec q - \vec p = \vec d \,\) (der Differenzvektor beider Stürzpunkte)
\(\, |\vec u| = u \,\)
\(\, |\vec d| = d \,\)
Aus unserer Gleichung wird dann:
\(\, (\vec q - \vec p + \lambda \cdot \vec u) \cdot \vec u = 0 \,\)
\(\, (\vec d + \lambda \cdot \vec u) \cdot \vec u = 0 \,\)
\(\, \vec d \cdot \vec u + \lambda \cdot (\vec u \cdot \vec u) = 0 \,\)
\(\, \vec d \cdot \vec u + \lambda \cdot |\vec u|^2 = 0 \,\)
\(\, \vec d \cdot \vec u + \lambda \cdot u^2 = 0 \,\)
Nach \(\, \lambda \,\) aufgelöst ergibt sich:
\(\, \lambda = - \frac{\vec d \cdot \vec u}{u^2} \,\)
Durch Einsetzen in Gleichung (1) erhalten wir die Formel für den Punkt \(\, S \,\):
\(\, \vec s = \vec q - \frac{\vec d \cdot \vec u}{u^2} \cdot \vec u \,\) (2)
Schritt 2: Berechnung der Länge \(\, a = |\overrightarrow{P S}| \,\)
Es gilt:
\(\, a = |\,\vec s - \vec p\,| \,\)
Für \(\, \vec s \,\) setzen wir den Term aus Gleichung (2) ein:
\(\, a = |\,\vec q - \frac{\vec d \cdot \vec u}{u^2} \cdot \vec u - \vec p\,| \,\)
\(\, = |\,\vec q - \vec p - \frac{\vec d \cdot \vec u}{u^2} \cdot \vec u\,| \,\)
\(\, = |\,\vec d - \frac{\vec d \cdot \vec u}{u^2} \cdot \vec u\,| \,\)
Vorübergehend ersetzen wir den Term \(\, \frac{\vec d \cdot \vec u}{u^2} \,\) durch \(\, \lambda \,\):
\(\, = |\,\vec d - \lambda \cdot \vec u\,| \,\)
\(\, = \sqrt{(\vec d - \lambda \cdot \vec u) \cdot (\vec d - \lambda \cdot \vec u)} \,\)
\(\, = \sqrt{(\vec d \cdot \vec d) - 2 \lambda \,(\vec d \cdot \vec u) + \lambda^2 \,(\vec u \cdot \vec u)} \,\)
\(\, = \sqrt{d^2 - 2 \lambda \,(\vec d \cdot \vec u) + \lambda^2 \,u^2} \,\)
Für \(\, \lambda \,\) setzen wir nun wieder den ursprünglichen Bruchterm ein:
\(\, = \sqrt{d^2 - 2 \frac{\vec d \cdot \vec u}{u^2} \,(\vec d \cdot \vec u) + (\frac{\vec d \cdot \vec u}{u^2})^2 \,u^2} \,\)
\(\, = \sqrt{d^2 - 2 \frac{\vec d \cdot \vec u}{u^2} \,(\vec d \cdot \vec u) + \frac{(\vec d \cdot \vec u)^2}{u^4} \,u^2} \,\)
\(\, = \sqrt{d^2 - 2 \frac{(\vec d \cdot \vec u)^2}{u^2} + \frac{(\vec d \cdot \vec u)^2}{u^2}} \,\)
\(\, = \sqrt{d^2 - \frac{(\vec d \cdot \vec u)^2}{u^2}} \,\)
\(\, = \sqrt{d^2 - \bigl( \frac{\vec d \cdot \vec u}{u} \bigr)^2} \,\) (3)
Damit wären wir fertig.
Wir bringen nun die Formeln für den Punkt \(\, S \,\) und den gesuchten Abstand \(\, a \,\) in die endgültige Form, indem wir die abkürzenden Schreibweisen wieder entfernen.
Aus Gleichung (2) ergibt sich die Formel für den Punkt \(\, S \,\):
\(\, \vec s = \vec q - \frac{(\vec q - \vec p) \cdot \vec u}{|\vec u|^2} \cdot \vec u \,\)
Und aus Gleichung (3) ergibt sich die Abstandsformel:
\(\, a = \sqrt{\left| \,\vec q - \vec p\, \right|^2 - \left( \frac{(\vec q - \vec p) \cdot \vec u}{|\vec u|} \right) ^2} \,\)
Diese Formeln gelten nicht nur im \(\, \mathbb{R}^3 \), sondern allgemein im \(\, \mathbb{R}^n \).