Seite zuletzt aktualisiert: 22.06.2023
Formulierung des Kosinussatzes
Der Kosinussatz ist eine Verallgemeinerung des Satzes von Pythagoras für beliebige (nicht unbedingt rechtwinklige) Dreiecke.
Die drei Varianten sind:
\(
a^2 = b^2 + c^2 - 2\,b\,c\cdot \cos \alpha \\
b^2 = a^2 + c^2 - 2\,a\,c\cdot \cos \beta \\
c^2 = a^2 + b^2 - 2\,a\,b\cdot \cos \gamma
\)
Ist z. B. in der dritten Variante der Winkel \(\, \gamma = 90° \), so ergibt sich der Satz von Pythagoras:
\( c^2 = a^2 + b^2 \)
* * *
Beweis
Der Beweis soll für die dritte Variante gezeigt werden:
\( c^2 = a^2 + b^2 - 2\,a\,b\cdot \cos \gamma \)
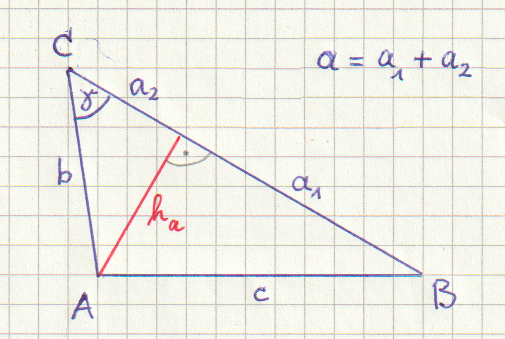
Das Ziel ist, die Seite c zu berechnen. Gegeben sind die Seiten a und b sowie der Winkel \(\gamma\,\).
Es gilt:
\( c^2 = a_1^2 + h_a^2 \,\). (1)
Für \( a_1 \) erhält man
\( a_1 = a - a_2 = a - b \cdot \cos \gamma \,\).
Für \( h_a \) erhält man
\( h_a = b \cdot \sin \gamma \,\).
Einsetzen in Gleichung (1) führt zu
\(
c^2 = (a - b \cdot \cos \gamma)^2 + b^2 \sin^2 \gamma \\
c^2 = (a - 2\,a\,b\cdot \cos \gamma + b^2 \cos^2 \gamma + b^2 \sin^2 \gamma \\
c^2 = a^2 + b^2(\sin^2 \gamma + \cos^2 \gamma) - 2\,a\,b \cdot \cos \gamma
\)
Da \(\, \sin^2 \gamma + \cos^2 \gamma = 1 \,\) ist (sog. trigonometrischer Pythagoras), folgt:
\(c^2 = a^2 + b^2 - 2\,a\,b\cdot \cos \gamma \)