Seite zuletzt aktualisiert: 23.06.2023
Ausgangssituation
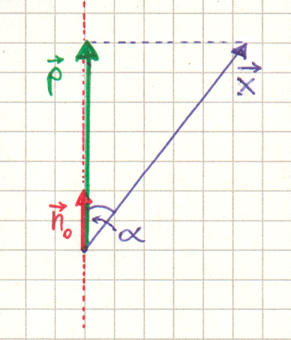
Gegeben sind die zwei Vektoren \( \vec x \) und \( \vec n_0\, \). Der Vektor \( \vec n_0 \) ist dabei ein Einheitsvektor (\( \,|\vec n_0 | = 1 \,\)).
Der Vektor \( \vec x \) soll auf die Richtung von \( \vec n_0 \) projiziert werden. Das Ergebnis sei der Vektor \( \vec p\, \).
Die Formel zur Berechnung von \( \vec p \) soll im Folgenden hergeleitet werden.
* * *
Vorüberlegung
\( \vec p \) muss ein Vielfaches von \( \vec n_0 \) sein:
\( \vec p = \lambda \cdot \vec n_0 \) (1)
Da \( \,|\vec n_0 | = 1 \,\) ist, ist der Betrag von \( \lambda \) gleich dem Betrag von \( \vec p \,\).
\( \lambda = |\vec p| \,\) oder \(\, \lambda = -|\vec p| \,\)
je nachdem, ob der Winkel \(\, \alpha \,\) kleiner oder größer als 90° ist.
* * *
Berechnung von \( \lambda \,\)
Im rechtwinkligen Dreieck (siehe Skizze oben) gilt für \(\, \alpha \le 90° \,\):
\( \cos \alpha = \frac{|\vec p|}{|\vec x|} \,\) bzw.
\(\, \cos \alpha = \frac{\lambda}{|\vec x|} \\ \Rightarrow \enspace \lambda = |\vec x| \cdot \cos \alpha \)
An der Formel ändert sich nichts, wenn man den Faktor \(\, |\vec n_0| = 1 \,\) hinzufügt:
\( \lambda = |\vec x| \cdot |\vec n_0| \cdot \cos \alpha \)
Auf der rechten Seite steht nun das Skalarprodukt der beiden Vektoren \( \vec x \) und \( \vec n_0 \,\) (siehe TEIL 2):
\( \lambda = \vec x \cdot \vec n_0 \) (2)
Durch Einsetzen in Formel (1) erhält man die Formel zur Berechnung des projizierten Vektors \( \vec p \,\):
\( \vec p = (\vec x \cdot \vec n_0) \cdot \vec n_0 \) (3)
Das Skalarprodukt hat den angenehmen Effekt, dass es bei \(\, \alpha > 90° \) negativ wird, und somit in diesem Fall auch genau das richtige Ergebnis liefert.
* * *
Projektionsformel für nicht normierte Vektoren
Wird ein Vektor \( \vec x \) auf die Richtung eines Vektors \( \vec n \) projiziert, der nicht normiert ist, d. h. \( |\vec n| \not= 1 \,\), folgt aus Formel (3):
\( \vec p = (\vec x \cdot \frac{\vec n}{|\vec n|}) \cdot \frac{\vec n}{|\vec n|} \)
\( \Rightarrow \) \( \vec p = \frac{\vec x \,\cdot\, \vec n}{|\vec n|^2 } \cdot \vec n \) (4)
* * *
Länge des projizierten Vektors \(\, \vec p \)
Aus Gleichung (3) folgt:
\( |\vec p| = |\vec x \cdot \vec n_0| \cdot |\vec n_0| = |\vec x \cdot \vec n_0| \)
Im Falle eines nicht normierten Vektors \(\, \vec n \,\) gilt dann:
\( |\vec p| = \frac{|\vec x \,\cdot\, \vec n|}{|\vec n| } \) (5)