Seite zuletzt aktualisiert: 30.08.2023
Schritt 1
Im Folgenden gilt:
\(|\vec a| = a\), \(|\vec b| = b\) und \(|\vec c| = c\,\).
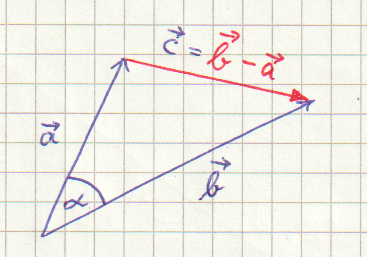
Nach dem sog. Kosinussatz der Trigonometrie (▸siehe TEIL 1) gilt:
\(c^2 = a^2 + b^2 - 2\,a\,b \cdot \cos \alpha\) (1)
\( \alpha\) ist dabei der Winkel zwischen den Seiten a und b eines Dreiecks.
Im Fall \( \alpha = 90°\) (rechtwinkliges Dreieck) erhält man als Spezialfall den Satz von Pythagoras.
* * *
Schritt 2
Nach der Vektorrechnung berechnet man für \( c^2 \, \):
\( c^2 = |\vec b - \vec a|^2 \\ = (b_1 - a_1)^2 + (b_2 - a_2)^2 + (b_3 - a_3)^2 \\ = b_1^2 - 2a_1b_1 + a_1^2 \enspace + \enspace b_2^2 - 2 a_2 b_2 + a_2^2 \enspace + \enspace b_3^2 - 2a_3b_3 + a_3^2 \\ = a_1^2 + a_2^2 + a_3^2 \enspace + \enspace b_1^2 + b_2^2 + b_3^2 \enspace - \enspace 2\,(a_1b_1 + a_2 b_2 + a_3b_3) \)
\(= |\vec a|^2 + |\vec b|^2 - 2\, (\vec a \cdot \vec b)\) (2)
* * *
Schritt 3
Vergleich von Gleichung (1) und Gleichung (2):
Schritt 1: \( c^2 = \:a^2 \:\, + \: b^2 \: - \: 2\, \color{red}{a\,b \cdot \cos \alpha} \)
Schritt 2: \( c^2 = |\vec a|^2 + |\vec b|^2 - 2\, (\color{red}{\vec a \cdot \vec b}) \)
Da die schwarzen Teile der beiden Formeln übereinstimmen, müssen zwangsläufig die beiden roten Teile ebenfalls gleich sein:
\( \vec a \cdot \vec b = a \, b \cdot \cos{\alpha} \)