Seite zuletzt aktualisiert: 23.06.2023
Aufgabenstellung
Von einem gegebenen Punkt X soll der Fußpunkt des Lotes auf die Ebene E (im \(\, \mathbb{R}^3 \,\)) bzw. auf die Gerade G (im \(\, \mathbb{R}^2 \,\)) berechnet werden.
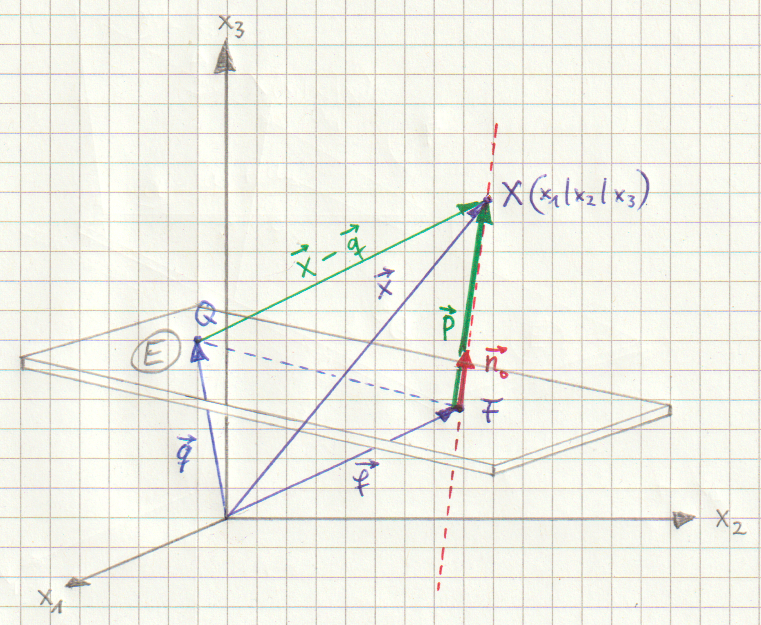
Im \(\, \mathbb{R}^3 \,\) sieht das so aus:
Im \(\, \mathbb{R}^2 \,\) sieht es fast genauso aus. Nur hat man jetzt eine Gerade G an Stelle der Ebene E:
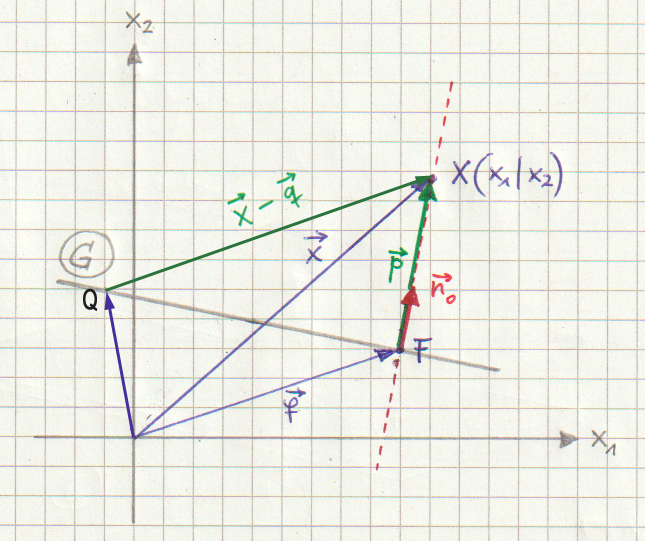
Berechnung
Die Rechnung gilt sowohl für den \(\, \mathbb{R}^2 \,\) als auch für den \(\, \mathbb{R}^3 \,\).
An der Zeichnung sieht man, dass für den Ortsvektor \( \vec f \) des Fusspunktes F gilt:
\( \vec f = \vec x - \vec p \) (1)
Der Vektor \( \vec p \) ist die Projektion des Vektors \( \vec x - \vec q \) auf die Normalenrichtung, wobei \( \vec q \) ein Stützvektor der Ebene bzw. der Geraden ist.
In die Formel (3) aus ▸TEIL 3 setzen wir für \( \vec x \) den Differenzvektor \( \vec x - \vec q \) ein und erhalten für den Vektor \( \vec p \):
\( \vec p = ((\vec x - \vec q) \cdot \vec n_0) \cdot \vec n_0 \)
Dies setzen wir nun in Gleichung (1) ein und erhalten für den Fußpunkt:
\( \vec f = \vec x - ((\vec x - \vec q) \cdot \vec n_0) \cdot \vec n_0 \)
Wenn \( \vec n \) nicht normiert ist, erhält man unter Verwendung der Formel (4) aus ▸TEIL 3:
\( \vec f = \vec x - \frac{(\vec x - \vec q) \,\cdot\, \vec n}{|\vec n|^2 } \cdot \vec n \)