Seite zuletzt aktualisiert: 06.11.2023
Polarkoordinaten
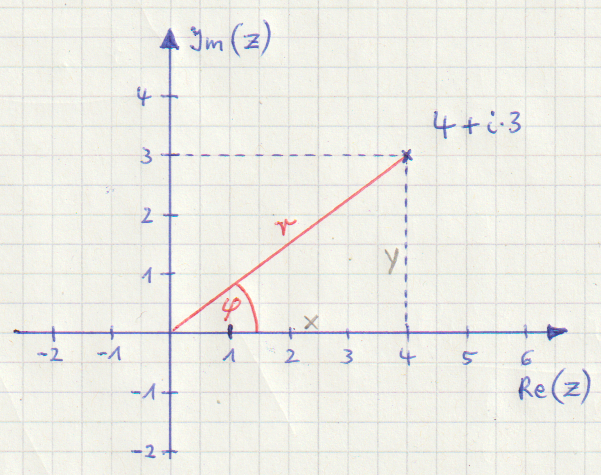
Anstatt den Ort eines Punktes in der zweidimensionalen Euklidischen Ebene durch einen x-Wert und einen y-Wert anzugeben, kann man seine Lage auch durch seine Entfernung vom Ursprung (Radius \( r \) ) und eine Richtung (Winkel \( \varphi \) ) eindeutig festlegen. Der Winkel \( \varphi \) wird dabei immer im Gegenuhrzeigersinn zur positiven x-Achse gemessen und nimmt Werte von 0 bis 360° an.
Die Zahlen \( r \) und \( \varphi \) nennt man die Polarkoordinaten des Punktes.
1. Umrechnung von Polarkoordinaten in kartesische Koordinaten:
Aus dem rechtwinkligen Dreieck mit den Seiten x, y, r und dem Winkel \( \varphi \) ergibt sich unmittelbar:
\( x = r \cdot cos\: \varphi \) (1)
\( y = r \cdot sin\: \varphi \) (2)
2. Umrechnung von kartesischen Koordinaten in Polarkoordinaten:
Die Berechnung des Radius' \( r \) ist unproblematisch:
\( r = \sqrt{x^2+y^2} \) (3)
\( r \) ist identisch mit dem Betrag der komplexen Zahl:
\( r = |\,z\,| \) .
Bei der Berechnung des Winkels \( \varphi \) wird eine Fallunterscheidung nötig, die je nach verwendeter Winkelfunktion unterschiedlich aussieht. Mein Favorit ist die Funktion \( arccos \) , weil die Fallunterscheidung in diesem Fall am übersichtlichsten ist.
Für komplexe Zahlen ungleich null gilt:
\( \varphi = \begin{cases} arccos(\frac{x}{r})\:, & y \ge 0 \\ 2\pi-arccos(\frac{x}{r})\:, & y < 0 \end{cases} \) (4)
Eine komplexe Zahl hat nach der Umrechnung in Polarkoordinaten die folgende Form:
\( r \cdot cos\: \varphi + i \cdot r \cdot sin\: \varphi \) (5)
Für die in der Zeichnung dargestellte komplexe Zahl \( 4+i \cdot 3 \) erhält man folgende Darstellung in Polarform:
\( 5 \cdot cos\, (36,9°) + i \cdot 5 \cdot sin\, (36,9°) \)
oder im Radialmaß:
\( 5 \cdot cos\, (0,6435) + i \cdot 5 \cdot sin\, (0,6435) \)
* * *
Eulersche Formel
Auf den ersten Blick ist der Vorteil der Polarkoordinaten nicht ersichtlich. Die Darstellung der komplexen Zahl scheint erst einmal komplizierter geworden zu sein. Erst wenn man die sog. Eulersche Formel ins Spiel bringt, erhält man eine überraschende Vereinfachung.
Klammert man in der Polarform
\( r \cdot cos\: \varphi + i \cdot r \cdot sin\: \varphi \)
den Faktor \( r \) aus, erhält man
\( r \cdot (cos\: \varphi + i \cdot sin\: \varphi) \) .
Die nach Leonhard Euler benannte Formel besagt nun, dass für alle \( \varphi \in \mathbb{R} \) gilt:
\( e^{\hspace{0.1em}i\hspace{0.1em}\varphi} = cos\: \varphi + i \cdot sin\: \varphi \) (6)
Diese Formel wird mit Hilfe der Reihenentwicklung (Taylor-Reihen) bewiesen (siehe ▸hier).
Die Polarform einer komplexen Zahl wird damit sehr kompakt:
\( r \cdot e^{\hspace{0.1em}i\hspace{0.1em}\varphi} \) (7)
Unsere Beispielzahl sähe dann so aus:
\( 5 \cdot e^{\hspace{0.1em}i\hspace{0.1em} \cdot 0,6435} \) (8)
Der Winkel \( \varphi \) ist hier im Radialmaß angegeben.
Nun ist offensichtlich, dass z. B. eine n-te Wurzel, d. h. eine Potenzierung mit \( \frac{1}{n} \) aufgrund der Potenzgesetze kein Problem mehr darstellt.
Mit dem Wurzelziehen aus komplexen Zahlen befasst sich der ▸Teil 3.