

Webseite zuletzt aktualisiert: 13.01.2026
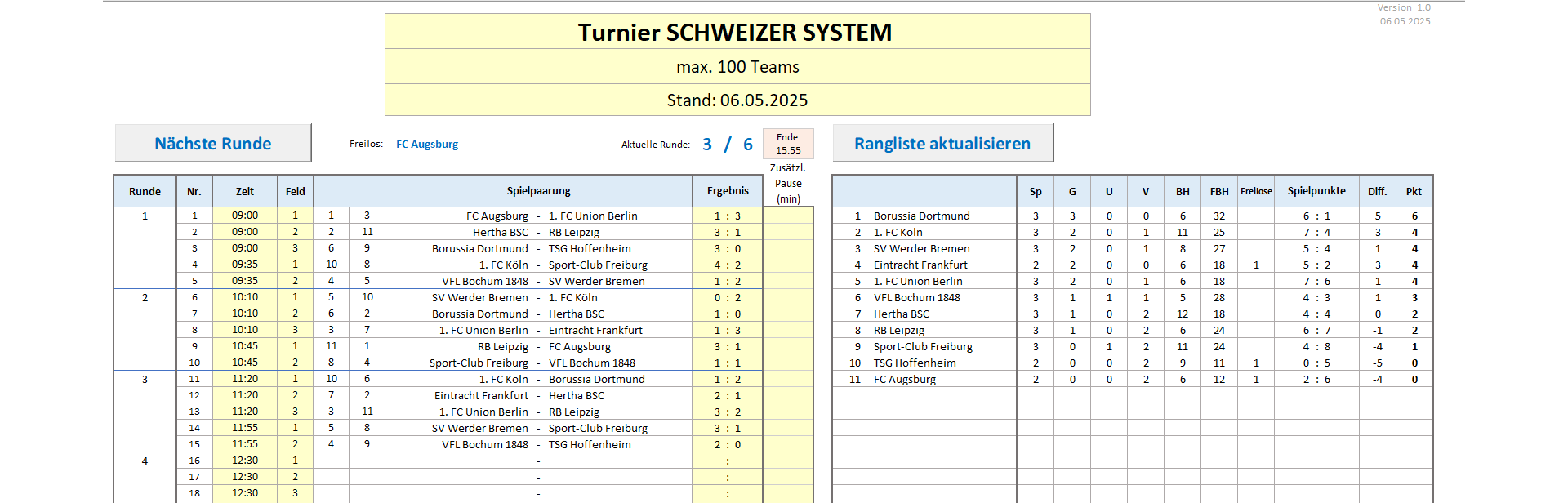
Vollautomatischer Excel-Turnierplan für ein Schweizer System, 4 bis 100 Teilnehmer, Anzahl der Runden frei wählbar, optional automatische Zeitplanung, optional automatisches Speichern zwischendurch, kein Passwortschutz - der VBA Code ist frei einsehbar.
NEU (seit 30.12.2025):
▸Rangliste übers ganze Jahr erstellen
NEU (seit Version 1.8 vom 04.12.2025):
Läuft jetzt auch auf dem Mac - vorausgesetzt, man hat Microsoft Excel installiert.
Da die komplizierte Auslosung der Spielrunden nur mit Programmierung (VBA Code) verwirklicht werden kann, enthält die Excel-Datei Makros und läuft deshalb nur mit Microsoft Excel (d.h. nicht mit Open Office Versionen).
Kostenloser Download - keine Werbung - alles offen und veränderbar - keine Nutzungseinschränkungen
In den Einstellungen kann man wählen,
Wenn das automatische Speichern eingeschaltet ist, wird nach jeder Rundenauslosung und nach jeder Aktualisierung der Rangliste automatisch gespeichert.
Bei einem der Turniere trat folgender Fall ein:
Nach Auslosung der Begegnungen für die nächste Runde stellte man fest, dass eines der Spielergebnisse falsch eingetragen war. Dies konnte zwar korrigiert werden und somit auch die Rangliste, aber die Auslosung der Begegnungen für die nächste Runde konnte nicht rückgängig gemacht werden bzw. mit dem nun richtigen Spielergebnis wiederholt werden.
Um für einen solchen Fall oder auch für andere Pannen Lösungsmöglichkeiten zu haben, kann man nun (ab Version 1.3) in den Einstellungen wählen, ob vor jeder Neuauslosung der Begegnungen automatisch eine Backup-Datei mit dem Stand der letzten Runde erstellt werden soll.
Für jede Backup-Datei werden das Wort "Runde" und die Rundennummer an den Namen der Originaldatei angehängt. Beim Originalnamen "2025-08-30_Turnier_Berlin.xlsm" heißt dann die Backup-Datei für die 4. Runde "2025-08-30_Turnier_Berlin_Runde_4.xlsm". Im Notfall hätte man damit die Möglichkeit, das Turnier mit dieser Datei fortzusetzen (am besten vorher umbenennen).
Bei einem anderen Turnier trat ein weiterer verbesserungsfähiger Punkt zutage:
Die 9 Spiele jeder Runde wurden in 3 verschiedenen Spielzeiten durchgeführt. Dabei trat der Fall ein, dass ein Team von einer Runde zur nächsten gar keine Pause hatte, während ein anderes Team das Maximum von 4 Spielzeiten Pause hatte.
Bei der Festlegung der Reihenfolge der ausgelosten Begegnungen wurden bisher die Anstoßzeiten der Teams in der vorhergehenden Runde nicht berücksichtigt. Dies ist nun ab der Version 1.5 behoben.
Außerdem wird ab Version 1.5 darauf geachtet, dass die Anzahl der "Heimspiele" (Team auf der linken Seite des Match-Plans) möglichst ausgewogen ist. Dieser Hinweis kam von einem Schachturnier. Dort ist es wichtig, dass es möglichst ausgewogen ist, wie oft die Teilnehmer die weißen Figuren haben und somit zuerst am Zug sind.
* * *
| Version | Datum | Beschreibung |
| 1.7 | 26.08.2025 | In den Einstellungen kann nun gewählt werden, ob bei der Berechnung des Heimvorteils (weiße Figuren im Schach) bei Gleichstand der Vorbedingungen das stärkere oder das schwächere Team bevorzugt wird. Die Statistik der Heim-/Auswärtsspiele kann jetzt angezeigt werden (einstellbar). Einige versteckte, im Normalbetrieb nicht auftretende Unstimmigkeiten wurden bereinigt. |
| 1.6 | 05.08.2025 | Fehler behoben: Nach dem Eintrag einer zusätzlichen Pause wurden (außer den Spielzeiten) fälschlicherweise auch die Spielfelder neu berechnet. Es werden jetzt nur noch die Spielzeiten neu berechnet. |
| 1.5 | 04.08.2025 | Berücksichtigung der Anstoßzeiten eines Teams aus der vorhergehenden Runde für die Reihenfolge der Spiele in der nächsten Runde. Ausgeglichene Anzahl von "Heimspielen" (weiße Figuren beim Schach) und "Auswärtsspielen" (schwarze Figuren beim Schach). |
| 1.4 | 01.08.2025 | Drei Änderungen:
|
| 1.3 | 31.07.2025 | Optional Erstellung einer Backup-Datei nach jeder Runde (vor der Auslosung der nächsten Runde) |
| 1.2 | 16.07.2025 | Die Eintragung von zusätzlichen Pausen bewirkt eine sofortige Änderung der Spielzeiten. (Man muss nicht mehr zusätzlich auf den Button "Zeitplan neu berechnen" klicken.) |
* * *
Die kleine Hilfsdatei "Overall_table_1.0_de.xlsm" erstellt auf Button-Klick eine Rangliste über alle bisher gesammelten Turniere nach dem Schweizer System. Die Datei liest einfach alle Turnierdateien aus, die im gleichen Unterverzeichnis liegen und erstellt eine Rangliste über alle diese Dateien.
▸Download der Hilfsdatei [78 kB], Version 1.0, erstellt am 30.12.2025
* * *
Wenn wir uns als Beispiel vorstellen, dass sich eine größere Anzahl Teilnehmer zu einem Turnier (Boole, Schach, Tischtennis, Dart, ...) trifft, wäre das KO-System der schnellste Weg, einen eindeutigen Sieger zu ermitteln. Bei 32 Teilnehmern sind genau 31 KO-Spiele erforderlich, um einen finalen Champion zu ermitteln.
Die Nachteile liegen auf der Hand: die Hälfte der Teilnehmer scheidet bereits nach dem ersten Spiel aus. Über die Rangreihenfolge der unteren Plätze hat das KO-System so gut wie keine Aussagekraft.
Das gerechteste System in dieser Hinsicht wäre ein Rundenturnier "Jeder gegen Jeden". Hierbei hat die Schlusstabelle eine große Aussagekraft über die Spielstärke der einzelnen Teilnehmer. Der Nachteil liegt auch auf der Hand: Bei 32 Teilnehmern wären 496 Spiele durchzuführen, was den Rahmen eines zeitlich begrenzten Turniers (z.B. Wochenendturnier) sprengen würde.
Das Schweizer System ist nun quasi ein Kompromiss zwischen diesen beiden Extremen. Obwohl beim Schweizer System oftmals nur KO-Spiele stattfinden, scheidet der Verlierer nicht aus, sondern spielt wie alle anderen Teilnehmer bis zum Schluss des Turniers mit. Er verliert somit nach der ersten Niederlage nicht gleich die Chance auf den Gesamtsieg.
Das Turnier wird wie beim "Jeder gegen Jeden" in sog. Runden durchgeführt (bei der Fußball-Bundesliga werden diese Runden "Spieltage" genannt). Bei 32 Teilnehmern besteht die erste Runde aus 16 Spielen, so dass jeder Teilnehmer nach der ersten Runde sein erstes Spiel gespielt hat. Bei einer ungeraden Anzahl von Teilnehmern setzt in jeder Runde ein Teilnehmer aus. Da dies per Los entschieden wird, spricht man hier auch von einem "Freilos".
Bei 32 Teilnehmern wären 31 Runden (Spieltage) nötig, um alle 496 Spiele durchzuführen.
Beim Schweizer System beschränkt man sich nun auf eine vorher festgelegte Anzahl von Runden.
Diese Anzahl sollte mindestens so groß sein wie die Anzahl der Runden in einem reinen KO-System. Bei 32 Teilnehmern wären genau 5 KO-Runden nötig, um einen Endsieger zu ermitteln. Deshalb wählt man beim Schweizer System meistens eine, zwei oder drei Runden mehr. In unserem Beispiel wäre also 7 Runden eine gute Wahl.
Und nun kommt das Besondere des Schweizer Systems: So wie im reinen KO-System in der nachfolgenden Runde Sieger auf Sieger treffen, die Erfolgreichen sozusagen unter sich sind, wird dies im Schweizer System dadurch erreicht, dass die Position in der Tabelle nach Ablauf einer jeden Runde bestimmt, gegen wen man in der nächsten Runde gelost wird. Steht man ziemlich weit oben in der Tabelle, erhält man in der folgenden Runde auch einen Gegner aus dem oberen Tabellenbereich. Steht man weit unten in der Tabelle, kann man damit rechnen, dass man in der nachfolgenden Runde auf einen entsprechend schwachen Gegner trifft.
Dies hat den Effekt, dass man bei einer großen Gruppe von Teilnehmern mit sehr unterschiedlichen Spielstärken spätestens nach zwei bis drei Runden auf relativ gleichwertige Gegner trifft, was den Spaß am Turnier erhöhen kann.
Eine Ausnahme bildet meistens die erste Runde. Hier werden die spielstärksten Teilnehmer gesetzt und werden ausnahmsweise gegen schwache Gegner gelost. Dadurch sammeln sich in der Tabelle die Spielstärkeren schon mal im oberen Tabellenbereich und die Spielschwächeren im unteren Tabellenbereich.
Erfunden wurde das Schweizer System im Jahr 1895 von dem Schweizer Julius Müller. Seitdem erfreut es sich wachsender Beliebtheit in allen möglichen Disziplinen, in denen zwei Personen oder zwei Mannschaften (oder neuerdings auch zwei Roboter) aufeinandertreffen. Besonders verbreitet ist das Schweizer System im Schach und im Pétanque, einer besonderen Form des Boole.
* * *
Es gibt sehr viele Varianten des Schweizer Systems, die an dieser Stelle nicht alle dargestellt werden können. Hier soll diejenige Variante genauer beschrieben werden, die in dieser Excel-Datei implementiert wurde.
Allen Varianten ist gemeinsam, dass nach jeder Runde die Rangliste aktualisiert wird und diese neue Rangfolge entscheidenden Einfluss auf die Auslosung der Begegnungen für die nachfolgende Runde hat. Alle Teilnehmer mit gleicher Punktzahl bilden einen sog. Los-Pool und werden für die nachfolgende Runde bevorzugt gegeneinander gelost.
Bei 32 Teilnehmern könnte z.B. die folgende Aufteilung vorliegen:
6 Teilnehmer haben 4 Punkte,
4 Teilnehmer haben 3 Punkte,
9 Teilnehmer haben 2 Punkte,
10 Teilnehmer haben 1 Punkt,
3 Teilnehmer haben 0 Punkte.
Dann werden aus den 6 Teilnehmern des obersten Pools 3 Paarungen per Losverfahren ermittelt, aus den 4 Teilnehmern des zweiten Pools 2 Paarungen, 5 weitere Paarungen aus den 9 Teilnehmern des dritten Pools, wobei hier ein Teilnehmer aus dem vierten Pool in den dritten Pool hochgelost wird, 5 weitere Paarungen mit den verbliebenen 9 Teilnehmern des vierten Pools, wobei 1 Teilnehmer aus dem letzten Pool in den vierten Pool hochgelost wird.
Doch so einfach wie an diesem Beispiel dargestellt ist es meistens nicht, denn bei diesem Verfahren sind eine ganze Reihe von Regeln vorgegeben, die in verschiedenen Varianten des Schweizer Systems leicht voneinander abweichen und die Durchführung der Paarungsfindung zu einem komplizierten Mechanismus machen.
Folgende Regeln werden bei der Auslosung einer Spielrunde beachtet:
In dieser Excel-Datei kann in der Teilnehmerliste für jeden Teilnehmer eine Spielstärke eingetragen werden (0 bis 9999), die bei der Auslosung der ersten Runde berücksichtigt wird. Sind keine Spielstärken vorgegeben, findet die Auslosung der ersten Runde rein zufällig statt.
Wer ein Spiel gewinnt, bekommt in der Fußball-Bundesliga 3 Punkte gut geschrieben. Bei einer Niederlage erhält man keine 3 Minuspunkte, weil dies überflüssig ist. Es würde im Endeffekt zu demselben Tabellenstand führen.
Es führt aber nur deshalb zu demselben Tabellenstand, weil am Ende der Saison alle Teilnehmer die gleiche Anzahl Spiele absolviert haben. Dies ist beim Schweizer System allerdings nicht immer der Fall. Bei ungerader Anzahl von Teilnehmern haben am Ende nicht alle die gleiche Anzahl von Spielen absolviert, weil in jeder Runde jemand aussetzt und nicht alle möglichen Runden ausgespielt werden. Bei 31 Teilnehmern und 7 Runden haben z.B. 7 Teilnehmer ein Spiel weniger als die restlichen 24 Teilnehmer.
In diesem Fall ist es für die Bestimmung der Rangfolge in der Schlusstabelle exakter, wenn man Plus- und Minuspunkte vergibt und als oberstes Kriterium nicht einfach nur die erreichten Pluspunkte nimmt, sondern die Differenz von Plus- und Minuspunkten. Warum?
Nehmen wir an, jemand hat nach drei Runden 2 Siege und eine Niederlage zu verzeichnen. Ein anderer hat einmal ausgesetzt und 2 Siege. Würde man für einen Sieg 1 Punkt vergeben, so hätten beide 2 Punkte und würden für die Auslosung der nachfolgenden Runde in demselben Pool landen.
Vergibt man Plus- und Minuspunkte, hätte der Erste einen Punktestand von 2:1, der zweite dagegen einen Punktestand von 2:0. Nimmt man die Punktdifferenz als oberstes Kriterium, würde der Erste im Pool der Teilnehmer mit einer Punktdifferenz von +1 landen, der Zweite jedoch im Pool mit Punktdifferenz von +2, was von der Einschätzung der bisherigen Ergebnisse gerechter wäre.
In dieser Excel-Datei kann man in den Einstellungen wählen, ob man die Punkte oder die Punktdifferenz verwendet.
In vielen Publikationen wird die Anzahl der Siege als oberstes Kriterium genannt. Dies ist meistens etwas zu einfach betrachtet, da in vielen Varianten des Schweizer Systems dem Aussetzer ein halber oder ganzer Sieg zugerechnet wird. Außerdem werden auch Varianten gespielt, bei denen ein Spiel unentschieden ausgehen kann, z.B. ein Remis im Schach. Hier werden 1 Punkt für einen Sieg und 0,5 Punkte für das Unentschieden vergeben.
In der Excel-Datei ist einstellbar, ob ein Unentschieden überhaupt möglich ist, und wenn ja, wie viele Punkte dafür gewertet werden.
Vielfach ist es üblich, dem Aussetzer entweder einen Sieg oder einen halben Sieg zuzurechnen. In der Excel-Datei kann man einstellen, wie viele Punkte für ein Aussetzen verrechnet werden. Auch null Punkte sind möglich.
* * *
Die Buchholzzahl wurde 1932 von dem Magdeburger Bruno Buchholz erfunden.
Was ist das und was hat es damit auf sich?
Wenn in der Fußball-Bundesliga ein Gleichstand in Punkten vorliegt, wird als nächstes Kriterium zur Ermittlung der Rangfolge in der Tabelle die Tordifferenz herangezogen. Dies ist ein gerechtes Vorgehen, weil am Ende der Saison alle Mannschaften gleichermaßen gegen alle stärkeren und alle schwächeren Gegner gespielt haben.
Es kann aber sehr ungerecht werden, wenn wie beim Schweizer System nicht alle Runden ausgespielt werden. So kann Team A vier Siege gegen vier sehr starke Gegner und Team B vier Siege gegen vier schwache Gegner errungen haben. Beide Teams haben dadurch dieselbe Punktzahl. Team B hat aufgrund der schwächeren Gegner eine bessere Tordifferenz und steht somit ungerechterweise in der Tabelle auf dem besseren Platz.
Aus diesem Grund wird beim Schweizer System eine Zahl errechnet, die wiedergibt, wie stark die Gegner von Team A und diejenigen von Team B waren. Dazu addiert man einfach die Punktzahlen aller Gegner des betreffenden Teams. Dabei werden nur die in echten Spielen erzielten Punkte berücksichtigt. Punkte, die z.B. für ein Freilos vergeben wurden, gehen nicht in die Berechnung ein. Diese Zahl nennt man die Buchholzzahl. An Stelle der Tordifferenz entscheidet die Buchholzzahl bei Punktgleichheit über die Platzierung in der Tabelle.
Stimmt auch die Buchholzzahl beider Teams überein, wird als noch feinere Unterwertung die sog. Feinbuchholzzahl herangezogen. Nehmen wir an, Team A und Team B haben beide die Buchholzzahl 18. Das bedeutet, dass die Gegner von Team A insgesamt 18 Punkte erreicht haben und die Gegner von Team B ebenso. Aber es könnte ja sein, dass die Gegner von Team A ihre Punkte auf einem leichteren Weg gesammelt haben als die Gegner von Team B, weil die Gegner von Team A insgesamt schwächere Gegner gehabt haben.
Somit entsteht die Idee, die Buchholzpunkte der Gegner von Team A zu addieren und mit der Summe der Buchholzpunkte der Gegner von Team B zu vergleichen. Diese Summe nennt man die Feinbuchholzzahl, weil sie eine noch feinere Unterwertung darstellt. Sie wird als drittes Kriterium zur Ermittlung der Rangfolge in der Tabelle verwendet.
In den weiteren Kriterien unterscheiden sich die verschiedenen Varianten des Schweizer Systems. In dieser Excel-Datei wird die Tordifferenz bzw. die Differenz der erreichten Spielpunkte/Satzpunkte als viertes Kriterium verwendet.
* * *
Die Komplexität des Losverfahrens bei der Paarungsfindung erzwingt den Einsatz einer Programmiersprache, in diesem Fall VBA (Visual Basic for Applications). Allein mit Formeln in den Zellen ist diese Aufgabe nicht zu bewältigen.
In dieser Excel-Datei wird die Paarungsfindung mit Hilfe eines Backtracking-Algorithmus' gelöst, der aus Performance-Gründen nicht rekursiv, sondern iterativ formuliert wurde. Für alle in der Praxis vorkommenden Fälle - selbst bei 100 Teilnehmern - reicht die Geschwindigkeit von VBA, um die Paarungen einer Spielrunde innerhalb von Bruchteilen einer Sekunde zu finden.
Erst wenn man versucht, bei einer größeren Anzahl von Teilnehmern (z.B. 45) über die übliche Anzahl von 7 - 10 Runden hinaus zu gehen, kann es passieren, dass bei der 17. oder bei der 19. Runde plötzlich eine sehr viel längere Zeit benötigt wird und Excel minutenlang eingefroren zu sein scheint.
Um dies zu verhindern, ist eine Begrenzung der Backtrackingschritte auf maximal 2 Mio. eingebaut (bei meinem Laptop mit einem älteren Intel I7-Prozessor ca. 2 sec). Wird diese Zahl bei der Suche nach den Paarungen überschritten, wird die Suche abgebrochen und die Meldung "OVERFLOW" erscheint.
Versucht man es noch einmal mit anderen Spielergebnissen, kann es passieren, dass auch die 17. und 19. Runde sehr zügig berechnet werden und darüber hinaus sogar die Paarungen aller 45 Runden (990 Spiele) ohne Probleme berechnet werden, so dass man sozusagen eine vollständige Liste aller Paarungen für ein Jeder-Gegen-Jeden-Turnier mit 45 Teilnehmern hat.
Wer damit etwas experimentieren möchte, kann die Konstante MAX_STEP_COUNT von 2 Mio. auf einen höheren Wert setzen. Sie ist am Anfang der Subroutine "Private Sub Paarungen" zu finden. Nach einer Änderung der Konstanten ist kein Neustart erforderlich, da es sich um eine lokal definierte Konstante handelt.
* * *
Weitere Excel-Turnierpläne:
▸https://hermann-baum.de/excel/Turnier/de
Wer etwas spenden möchte,
hat hier eine Möglichkeit dazu: