

Website last updated: 13.01.2026
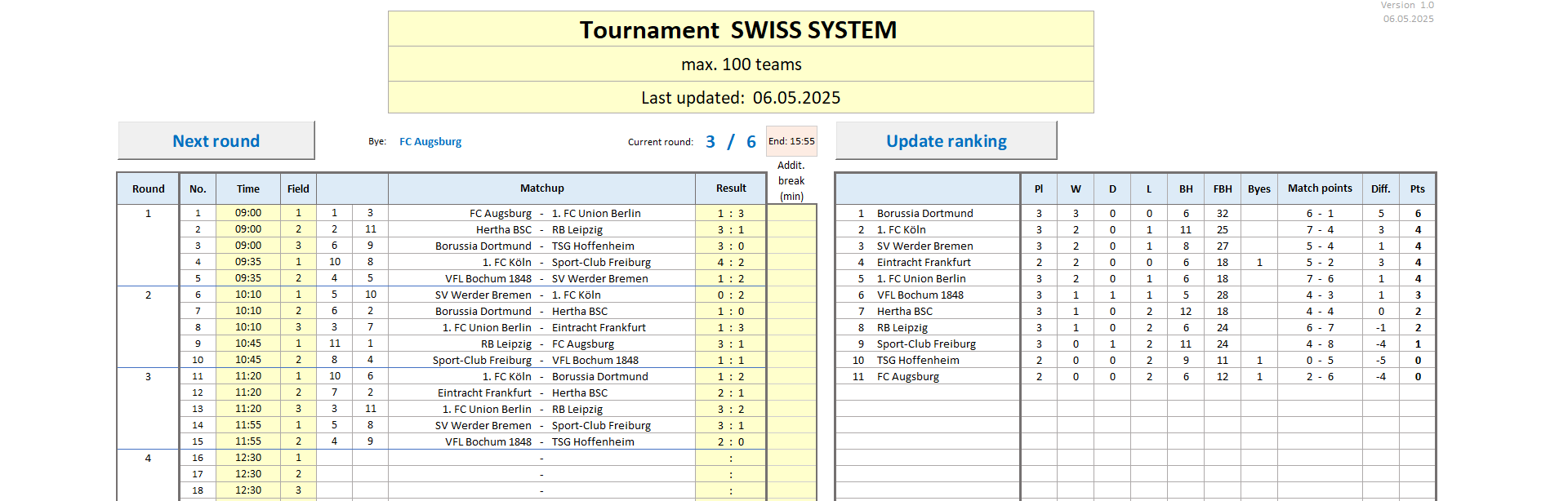
Fully automatic Excel tournament schedule for a Swiss system, 4 to 100 participants, number of rounds freely selectable, optional automatic scheduling, optional automatic saving in between, no password protection - the VBA code is freely visible.
NEW (since 30.12.2025):
▸Create a ranking for the entire year
NEW (since version 1.8 from 04.12.2025):
It now also runs on Mac - provided you have Microsoft Excel installed.
Since the complicated drawing of the game rounds can only be realized with programming (VBA code), the Excel file contains macros and therefore only runs with Microsoft Excel (i.e. not with Open Office versions).
Free download - no advertising - everything open and modifiable - no usage restrictions
In the settings, you can choose
If automatic saving is enabled, the Excel file will be saved automatically after each round draw and after each ranking update.
The following case occurred in one of the tournaments:
After the draw for the next round, it was discovered that one of the match results had been entered incorrectly. This could be corrected, and thus the rankings, but the draw for the next round could not be reversed or repeated with the correct match result.
To provide solutions for such a case or other glitches, you can now (as of version 1.3) choose in the settings whether a backup file containing the status of the last round should be automatically created before each new draw for the matches.
For each backup file, the word "Round" and the round number are appended to the name of the original file. With the original name "2025-08-30_Tournament_London.xlsm," the backup file for the 4th round would then be called "2025-08-30_Tournament_London_Round_4.xlsm." In an emergency, this would allow the tournament to continue with this file (preferably renamed beforehand).
At another tournament, another point for improvement emerged:
The 9 games of each round were played over 3 different periods. In some cases, one team had no break at all from one round to the next, while another team had the maximum of 4 game periods.
When determining the order of the drawn matches, the kickoff times of the teams in the previous round were previously not taken into account. This has been resolved starting with version 1.5.
Furthermore, starting with version 1.5, care is taken to ensure that the number of "home games" (teams on the left side of the match plan) is as balanced as possible. This suggestion came from a chess tournament. There, it's important to balance the number of times participants have the white pieces and thus move first.
* * *
| Version | Date | Description |
| 1.7 | 26.08.2025 | In the settings, you can now choose whether the stronger or weaker team is favored when calculating home advantage (white pieces in chess) in the event of a tie. Statistics for home/away games can now be displayed (adjustable). Some hidden inconsistencies that do not occur during normal operation have been resolved. |
| 1.6 | 05.08.2025 | Bug fixed: After entering an additional break, the playing fields (in addition to the playing times) were also incorrectly recalculated. Now, only the playing times are recalculated. |
| 1.5 | 04.08.2025 | Taking into account the kick-off times of a team from the previous round for the order of matches in the next round. As balanced as possible number of "home games" (white pieces in chess) and "away games" (black pieces in chess). |
| 1.4 | 01.08.2025 | Three changes:
|
| 1.3 | 31.07.2025 | Optional creation of a backup file after each round (before the draw for the next round) |
| 1.2 | 16.07.2025 | Entering additional breaks now results in an immediate change in playing times. (You no longer have to click the "Calculate schedule" button.) |
* * *
The small helper file "Overall_table_1.0_en.xlsm" creates a ranking list of all tournaments collected so far according to the Swiss system when a button is clicked. The file simply reads all tournament files located in the same subdirectory and creates a ranking list of all these files.
▸Download the helper file [78 kB], version 1.0, created on 30.12.2025
* * *
If we imagine, for example, a large number of participants meeting for a tournament (Boule, chess, table tennis, darts, etc.), the fastest way to determine a clear winner would be the knockout system. With 32 participants, exactly 31 knockout matches are required to determine a final champion.
The disadvantages are obvious: half of the participants are eliminated after the first game. The knockout system has virtually no significance regarding the ranking of the lower places.
The fairest system in this regard would be a round-robin tournament. The final standings are highly informative about the playing strength of the individual participants. The disadvantage is also obvious: With 32 participants, 496 games would have to be played, which would exceed the scope of a time-limited tournament (e.g., a weekend tournament).
The Swiss system is essentially a compromise between these two extremes. Although the Swiss system often only involves knockout matches, the loser is not eliminated but continues to play until the end of the tournament like all other participants. Thus, they do not immediately lose their chance of overall victory after the first loss.
The tournament, like a "round robin", is played in so-called rounds (in the Premier League, these rounds are called "matchdays"). With 32 participants, the first round consists of 16 games, so that every participant has played their first game after the first round. With an odd number of participants, one participant takes a break in each round (a "bye", decided by drawing lots).
With 32 participants, 31 rounds (matchdays) would be necessary to complete all 496 matches.
The Swiss system limits the number of rounds to a predetermined number.
This number should be at least as large as the number of rounds in a pure knockout system. With 32 participants, exactly 5 knockout rounds would be necessary to determine a final winner. Therefore, one, two, or three more rounds are usually chosen in the Swiss system. In our example, 7 rounds would be a good choice.
And now comes the special feature of the Swiss system: Just as in the pure knockout system, winners face winners in the following round, so to speak, the successful ones are among themselves, in the Swiss system this is achieved by the fact that the position in the table after each round determines who you are drawn against in the next round. If you're fairly high in the table, you'll face an opponent from the upper half of the table in the following round. If you're far down in the table, you can expect to face a correspondingly weaker opponent in the next round.
This has the effect that, in a large group of participants with very different skill levels, you'll encounter relatively equal opponents after two or three rounds at the latest, which can increase the fun of the tournament.
The first round is usually an exception. Here, the strongest players are seeded and, as an exception, are drawn against weaker opponents. This means that the stronger players tend to cluster in the upper half of the table, while the weaker players cluster in the lower half.
The Swiss system was invented in 1895 by the Swiss Julius Müller. Since then, it has enjoyed growing popularity in all kinds of disciplines involving two people or two teams (or, more recently, two robots). The Swiss system is particularly popular in chess and pétanque, a special form of Boole.
* * *
There are many variations of the Swiss System, and not all of them can be presented here. Here, the variation implemented in this Excel file will be described in more detail.
All variations have in common that the rankings are updated after each round, and this new ranking has a decisive influence on the draw for the following round. All participants with the same number of points form a so-called drawing pool and are drawn against each other with priority for the next round.
For example, with 32 participants, the following distribution could apply:
6 participants have 4 points,
4 participants have 3 points,
9 participants have 2 points,
10 participants have 1 point,
3 participants have 0 points.
Then, 3 pairings are determined by lot from the 6 participants in the top pool, 2 pairings from the 4 participants in the second pool, 5 additional pairings from the 9 participants in the third pool, with one participant from the fourth pool being drawn up to the third pool, and 5 additional pairings with the remaining 9 participants in the fourth pool, with one participant from the last pool being drawn up to the fourth pool.
But it's usually not as simple as this example suggests, because this procedure is subject to a whole series of rules that vary slightly in different variations of the Swiss system, making the pairing process a complicated mechanism.
The following rules are observed when drawing a round:
In this Excel file, a playing strength can be entered for each player in the participant list (0 to 9999), which will be taken into account in the first-round draw. If no playing strengths are specified, the first-round draw will take place purely at random.
Winning a match in the Premier League is awarded 3 points. A loss doesn't deduct 3 points, as this is unnecessary. It would ultimately result in the same standings.
However, this only results in the same standings because at the end of the season, all participants have played the same number of matches. This isn't always the case with the Swiss system. With an odd number of participants, not everyone has played the same number of matches at the end because someone sits out each round and not all possible rounds are played. With 31 participants and 7 rounds, for example, 7 participants have one fewer match than the remaining 24 participants.
In this case, it is more accurate to determine the ranking in the final standings if you award plus and minus points and use the difference between plus and minus points as the primary criterion, not simply the plus points achieved. Why?
Let's assume someone has two wins and one loss after three rounds. Another has one bye and two wins. If one were to award one point for a win, both would have two points and would end up in the same pool for the draw for the next round.
If plus and minus points were awarded, the first would have a score of 2:1, while the second would have a score of 2:0. If the point difference were used as the primary criterion, the first would end up in the pool of participants with a point difference of +1, while the second would end up in the pool with a point difference of +2, which would be fairer based on the assessment of previous results.
In this Excel file, you can choose whether to use points or point difference in the settings.
Many publications cite the number of wins as the primary criterion. This is often viewed somewhat too simply, as in many variations of the Swiss system, a player who takes a break (a bye) is awarded half or a full win. There are also variations where a game can end in a draw, such as a draw in chess. Here, 1 point is awarded for a win and 0.5 points for a draw.
In the Excel file, you can specify whether a draw is even possible and, if so, how many points are awarded for it.
It is often customary to award a player who takes a break (a bye) either a win or a half win. In the Excel file, you can specify how many points are awarded for a bye. Zero points are also possible.
* * *
The Buchholz Number was invented in 1932 by Bruno Buchholz of Magdeburg.
What is it and what does it mean?
If there is a tie in points in the Premier League, the next criterion for determining the ranking in the table is goal difference. This is a fair approach because at the end of the season, all teams have played equally against all stronger and weaker opponents.
However, it can become very unfair if, as in the Swiss system, not all rounds are played. For example, Team A may have four wins against four very strong opponents, and Team B may have four wins against four weaker opponents. Both teams therefore have the same number of points. Team B has a better goal difference due to the weaker opponents and is therefore unfairly ranked higher in the table.
For this reason, the Swiss system calculates a number that reflects the strength of Team A's and Team B's opponents. This is done by simply adding together the points totals of all of the team's opponents. Only points earned in actual matches are taken into account. Points awarded, for example, for a bye, are not included in the calculation. This number is called the Buchholz number. Instead of the goal difference, the Buchholz number determines the ranking in the table in the event of a tie.
If the Buchholz number of both teams is also the same, the so-called fine Buchholz number is used as an even more refined sub-score. Let's assume that Team A and Team B both have a Buchholz number of 18. This means that Team A's opponents have achieved a total of 18 points, and Team B's opponents have achieved the same number. However, it could be that Team A's opponents earned their points more easily than Team B's opponents because Team A's opponents faced weaker opponents overall.
This gives rise to the idea of adding the Buchholz points of Team A's opponents and comparing them with the sum of the Buchholz points of Team B's opponents. This sum is called the fine Buchholz number because it represents an even more refined sub-score. It is used as the third criterion for determining the ranking in the table.
The various variants of the Swiss system differ in the other criteria. In this Excel file, the goal difference or the difference in the achieved match points/set points is used as the fourth criterion.
* * *
The complexity of the random pairing process requires the use of a programming language, in this case VBA (Visual Basic for Applications). This task cannot be accomplished using formulas in the cells alone.
In this Excel file, the pairing process is solved using a backtracking algorithm that, for performance reasons, was formulated iteratively rather than recursively. For all practical cases - even with 100 participants - VBA's speed is sufficient to find the pairings for a match round within fractions of a second.
Only when you try to go beyond the usual number of 7-10 rounds with a larger number of participants (e.g., 45), it can happen that the 17th or 19th round suddenly takes a much longer time, and Excel seems to freeze for minutes.
To prevent this, a limit of 2 million backtracking steps is built in (about 2 seconds on my laptop with an older Intel I7 processor). If this number is exceeded when searching for pairings, the search is aborted and the message "OVERFLOW" appears.
If you try again with different game results, it can happen that the pairings for all 45 rounds (990 games) are calculated without problems, so that you have, so to speak, a complete list of all pairings for a round-robin tournament with 45 participants.
If you want to experiment with this, you can set the constant MAX_STEP_COUNT from 2 million to a higher value. It can be found at the beginning of the "Private Sub Pairings" subroutine. Changing the constant does not require a restart, as it is a locally defined constant.
* * *
More Excel tournament schedules:
▸https://hermann-baum.de/excel/Turnier/en
If you would like to donate something,
you can do so here: